题目内容
已知函数
(1)若直线 是曲线
是曲线 的切线,求
的切线,求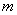 的值;
的值;
(2)若直线 是曲线
是曲线 的切线,求
的切线,求 的最大值;
的最大值;
(3)设 是曲线
是曲线 上相异三点,其中
上相异三点,其中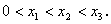
求证:
解:(1)设切点为(x0,lnx0), k=f¢(x)= 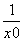 =
= 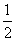 ,x0 = 2 ,\切点为(2,ln2),
,x0 = 2 ,\切点为(2,ln2),
代入y= 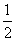 x + m得:m = ln2-1.----------------4分
x + m得:m = ln2-1.----------------4分
(2)设y = ax+b切f(x)于(t,lnt)(t>0), f¢(x)= 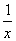 , \ f¢(t)=
, \ f¢(t)= 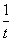 ,
,
则切线方程为:y = 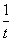 (x-t)+lnt ,y =
(x-t)+lnt ,y = 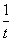 x+lnx-1 , a=
x+lnx-1 , a= 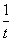 ,b= lnt-1
,b= lnt-1
\ab= 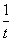 (lnt-1), 令g(t)=
(lnt-1), 令g(t)= 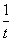 (lnt-1), g¢(t)= -
(lnt-1), g¢(t)= - 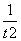 (lnt-1)+
(lnt-1)+ 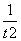 =
= 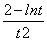
若tÎ(0,e2)时,g¢(t)>0,\ g(t)在(0,e2)上单调增;tÎ(e2,+¥)时,g¢(t)<0, \ g(t)在(e2,+¥)上单调递减;所以,当t= e2时,ab的最大值为:
g(e2)= 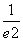 (lne2-1)=
(lne2-1)= 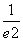 ------------------------8分
------------------------8分
(3)先证: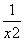 <
<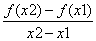 <
< 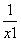 ,即证:
,即证: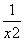 <
<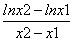 <
< 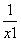 ,
,
只证:1- 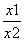 <ln
<ln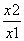 <
< 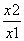 - 1 , 令
- 1 , 令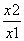 = t >1, 设h(m) =lnt–t +1 ,
= t >1, 设h(m) =lnt–t +1 ,
h¢(m)= 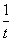 - 1<0 , 所以:h(t)在(1,+ ¥)上单调递减,则h(t)<h(1)=ln1-1+1=0,
- 1<0 , 所以:h(t)在(1,+ ¥)上单调递减,则h(t)<h(1)=ln1-1+1=0,
即证:ln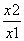 <
< 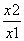 – 1. 以下证明:1-
– 1. 以下证明:1- 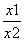 <ln
<ln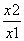
令p(t)= lnt+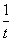 -1 , p¢(t)=
-1 , p¢(t)= 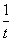 -
- 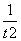 >0 , 所以:p(t)= lnt+
>0 , 所以:p(t)= lnt+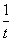 -1在(1,+ ¥)上单调递增,即:p(t)>p(1)= 0 ,即有:lnt+
-1在(1,+ ¥)上单调递增,即:p(t)>p(1)= 0 ,即有:lnt+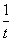 -1>0, \1-
-1>0, \1- 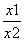 <ln
<ln 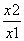 获证.
获证.
故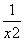 <
<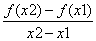 <
< 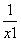 成立 ,同理可证:
成立 ,同理可证: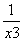 <
<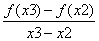 <
< 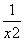 ,综上可知::
,综上可知::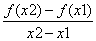 >
> 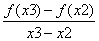 成立------------12分
成立------------12分

班主任为了对本班学生的考试成绩进行分析,决定从全班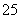 名女同学,
名女同学,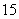 名男同学中随机抽取一个容量为
名男同学中随机抽取一个容量为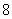 的样本进行分析.随机抽出
的样本进行分析.随机抽出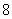 位,他们的数学分数从小到大排序是:
位,他们的数学分数从小到大排序是: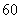 、
、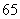 、
、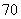 、
、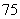 、
、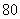 、
、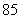 、
、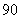 、
、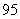 ,物理分数从小到大排序是:
,物理分数从小到大排序是: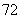 、
、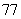 、
、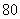 、
、 、
、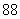 、
、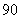 、
、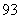 、
、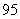 .
.
(Ⅰ)若规定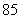 分以上(包括
分以上(包括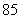 分)为优秀,求这
分)为优秀,求这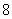 位同学中恰有
位同学中恰有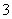 位同学的数学和物理分数均为优秀的概率;
位同学的数学和物理分数均为优秀的概率;
(Ⅱ)若这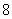 位同学的数学、物理分数对应如下表:
位同学的数学、物理分数对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
根据上表数据用变量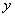 与
与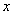 的相关系数或散点图说明物理成绩
的相关系数或散点图说明物理成绩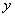 与数学成绩
与数学成绩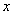 之间是否具有线性相关性?如果具有线性相关性,求
之间是否具有线性相关性?如果具有线性相关性,求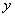 与
与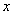 的线性回归方程(系数精确到
的线性回归方程(系数精确到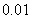 );如果不具有线性相关性,请说明理由.
);如果不具有线性相关性,请说明理由.
参考公式:相关系数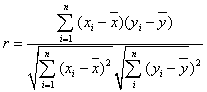 ;回归直线的方程是:
;回归直线的方程是: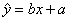 .
.
其中对应的回归估计值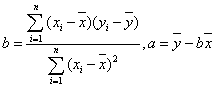 ;
;
参考数据: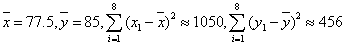 ;
;
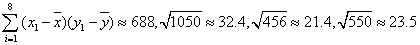
 的展开式中的常数项是________.
的展开式中的常数项是________.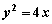 上一点,
上一点, 是焦点,且
是焦点,且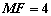 .过点
.过点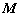 作准线
作准线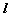 的垂线,垂足为
的垂线,垂足为
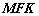 的面积为 .该抛物线的焦点与双曲线
的面积为 .该抛物线的焦点与双曲线 的一个焦点相同,且双曲线的离心率为2,那么该双曲线
的一个焦点相同,且双曲线的离心率为2,那么该双曲线 分别是方程
分别是方程 和
和 的根(其中
的根(其中 ), 则
), 则 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D. 
 , 若
, 若 且
且 (a,b,cR),则实数
(a,b,cR),则实数 的取值范围是
的取值范围是  ,则
,则  在
在 处的导数
处的导数 =( )
=( ) B.-
B.- C.0 D.
C.0 D.
 B.100 C.20 D.
B.100 C.20 D. 
 ,若
,若 ,则
,则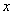 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.