题目内容
（2012•唐山二模）在△ABC中，三边对应的向量满足（
-3
)⊥
⊥
，则角A的最大值为
．
| AB |
| AC |
| CB |
| CB |
| π |
| 6 |
| π |
| 6 |
分析：由题意可得 (
-3
)•
=0，化简得ac•cosB-3ab•cos（π-C）=0，再利用正弦定理求得tanC=-3tanB，判断A为锐角，故 tanA＞0，利用基本不等式求得tanA≤
，由此求得A的最大值．
| AB |
| AC |
| CB |
| ||
| 3 |
解答：解：在△ABC中，（
-3
)⊥
⊥
，∴(
-3
)•
=0．
即
•
-3
•
=0，即ac•cosB-3ab•cos（π-C）=0．
化简可得
=-
，∴
=-
，解得tanC=-3tanB，
故tanC与tanB符号相反，故 B或C中有一个为钝角，故A为锐角，故 tanA＞0．
∴tanA=-tan（B+C）=
=
=
＞0，
故有tanB＞0，再由基本不等式可得
≤
，即tanA≤
，故A的最大值为
，
故答案为
．
| AB |
| AC |
| CB |
| CB |
| AB |
| AC |
| CB |
即
| AB |
| CB |
| AC |
| CB |
化简可得
| b |
| c |
| 1 |
| 3 |
| cosB |
| cosC |
| sinB |
| sinC |
| 1 |
| 3 |
| cosB |
| cosC |
故tanC与tanB符号相反，故 B或C中有一个为钝角，故A为锐角，故 tanA＞0．
∴tanA=-tan（B+C）=
| tanB+tanC |
| tanB•tanC-1 |
| 2tanB |
| 1+3tan2B |
| 2 | ||
|
故有tanB＞0，再由基本不等式可得
| 2 | ||
|
| ||
| 3 |
| ||
| 3 |
| π |
| 6 |
故答案为
| π |
| 6 |
点评：本题主要考查两个向量垂直的性质，两个向量的数量积的定义，正弦定理以及基本不等式的应用，属于中档题．
练习册系列答案
相关题目
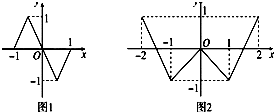（2012•唐山二模）奇函数f（x）、偶函数g（x）的图象分别如图1、2所示，方程f（g（x））=0、g（f（x））=0的实根个数分别为a、b，则a+b=（ ）