题目内容
已知{an}是一个等差数列，且a2=1，a5=-5．（Ⅰ）求{an}的通项an；
（Ⅱ）求{an}前n项和Sn的最大值．
【答案】分析：（1）用两个基本量a1，d表示a2，a5，再求出a1，d．代入通项公式，即得．
（2）将Sn的表达式写出，是关于n的二次函数，再由二次函数知识可解决之．
解答：解：（Ⅰ）设{an}的公差为d，由已知条件，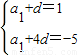
，
解出a1=3，d=-2，所以an=a1+（n-1）d=-2n+5．
（Ⅱ）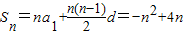
=4-（n-2）2．
所以n=2时，Sn取到最大值4．
点评：本题是对等差数列的基本考查，先求出两个基本量a1和d，其他的各个量均可以用它们表示．
（2）将Sn的表达式写出，是关于n的二次函数，再由二次函数知识可解决之．
解答：解：（Ⅰ）设{an}的公差为d，由已知条件，
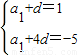，解出a1=3，d=-2，所以an=a1+（n-1）d=-2n+5．
（Ⅱ）
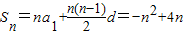=4-（n-2）2．所以n=2时，Sn取到最大值4．
点评：本题是对等差数列的基本考查，先求出两个基本量a1和d，其他的各个量均可以用它们表示．
练习册系列答案
小题狂做系列答案
相关题目