题目内容
设集合 ,若A∩B=A,求实数a的取值范围.
,若A∩B=A,求实数a的取值范围.
【答案】分析:解绝对值不等式可求出集合A,解分式不等式可以求出集合B,由A∩B=A可得A⊆B,结合集合包含关系定义,可构造关于a的不等式组,解得实数a的取值范围.
解答:解:若|x-a|<2,则-2<x-a<2,即a-2<x<a+2
故A={x||x-a|<2}={x|a-2<x<a+2}.…(3分)
若 ,则
,则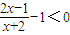 ,即
,即 ,即-2<x<3
,即-2<x<3
 .…(7分)
.…(7分)
因为A∩B=A,即A⊆B,
所以 .
.
解得0≤a≤1,…(11分)
故实数a的取值范围为[0,1]…(12分)
点评:本题考查的知识点是集合关系中的参数取值问题,其中解绝对值不等式和分式不等式求出集合A,B是解答本题的关键.
解答:解:若|x-a|<2,则-2<x-a<2,即a-2<x<a+2
故A={x||x-a|<2}={x|a-2<x<a+2}.…(3分)
若
 ,则
,则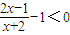 ,即
,即 ,即-2<x<3
,即-2<x<3 .…(7分)
.…(7分)因为A∩B=A,即A⊆B,
所以
 .
.解得0≤a≤1,…(11分)
故实数a的取值范围为[0,1]…(12分)
点评:本题考查的知识点是集合关系中的参数取值问题,其中解绝对值不等式和分式不等式求出集合A,B是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若A∪B=A,求a的值组成的集合.
,若A∪B=A,求a的值组成的集合. ,若A∪B=A,求a的值组成的集合.
,若A∪B=A,求a的值组成的集合.
 ,若A∩B=A,求实数a的取值范围.
,若A∩B=A,求实数a的取值范围. ,若A∩B=A,求实数a的取值范围.
,若A∩B=A,求实数a的取值范围.