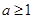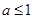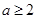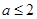题目内容
过原点且倾斜角为60°的直线与圆:x2+y2-4y=0的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.无法确定 |
∵直线的倾斜角为60°,∴直线的斜率k=tan60°=
,
结合直线过原点,得直线方程为y=
x,即
x-y=0
∵圆x2+y2-4y=0,即x2+(y-2)2=4,
得圆心为(0,2),半径r=2.
∴圆心到直线的距离d=
=1<2,
∴直线与圆:x2+y2-4y=0的位置关系是:相交.
故选:B.
| 3 |
结合直线过原点,得直线方程为y=
| 3 |
| 3 |
∵圆x2+y2-4y=0,即x2+(y-2)2=4,
得圆心为(0,2),半径r=2.
∴圆心到直线的距离d=
| |-2| | ||||
|
∴直线与圆:x2+y2-4y=0的位置关系是:相交.
故选:B.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
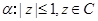 ,
, .若
.若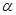 是
是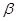 的充分非必要条件,则实数
的充分非必要条件,则实数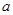 的取值范围是( )
的取值范围是( )