题目内容
在边长为2的正方形内随机地取一点，则该点到正方形中心的距离小于1的概率为
．
| π |
| 4 |
| π |
| 4 |
分析：根据题意，分析可得所有到正方形中心的距离小于1的点均在以O圆心的单位圆内，分别求出正方形与圆的面积，由几何概率公式，计算可得答案．
解答：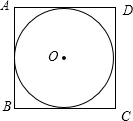
解：如图，正方形ABCD的边长为2，其中心为O，
所有到正方形中心O的距离小于1的点均在以O为圆心，半径为1的单位圆内，
故所求概率为该圆与该正方形的面积之比，
易得S正方形=2×2=4，
S圆=π×12=π，
故其概率为
．
解：如图，正方形ABCD的边长为2，其中心为O，所有到正方形中心O的距离小于1的点均在以O为圆心，半径为1的单位圆内，
故所求概率为该圆与该正方形的面积之比，
易得S正方形=2×2=4，
S圆=π×12=π，
故其概率为
| π |
| 4 |
点评：本题考查几何概型的计算，关键是审清题意，明确符合条件的点的区域．
练习册系列答案
相关题目
