题目内容
若x∈R,y∈R,且|x|≤4,|y|≤3,求点P(x,y)落在椭圆
+
=1内的概率(参考公式:当椭圆的长半轴长为a,短半轴长为b时,椭圆围成的区域的面积为 abπ)( )
| x2 |
| 16 |
| y2 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:平面区域Ω:x∈R,y∈R,且|x|≤4,|y|≤3,是一个矩形区域,如图所示.依题意及几何概型,可得
=
,由此可导出椭圆M的方程.
| πab | ||
8
|
| π |
| 4 |
解答:解 :平面区域Ω:x∈R,y∈R,且|x|≤4,|y|≤3,是一个矩形区域,如图所示.
:平面区域Ω:x∈R,y∈R,且|x|≤4,|y|≤3,是一个矩形区域,如图所示.
依题意及几何概型,可得
=
,
所以,点P(x,y)落在椭圆
+
=1内的概率
.
故选D.
 :平面区域Ω:x∈R,y∈R,且|x|≤4,|y|≤3,是一个矩形区域,如图所示.
:平面区域Ω:x∈R,y∈R,且|x|≤4,|y|≤3,是一个矩形区域,如图所示.依题意及几何概型,可得
| πab |
| 2×3 |
| π |
| 4 |
所以,点P(x,y)落在椭圆
| x2 |
| 16 |
| y2 |
| 9 |
| π |
| 4 |
故选D.
点评:此题考查学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
相关题目
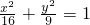 内的概率(参考公式:当椭圆的长半轴长为a,短半轴长为b时,椭圆围成的区域的面积为 abπ)
内的概率(参考公式:当椭圆的长半轴长为a,短半轴长为b时,椭圆围成的区域的面积为 abπ)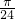



 内的概率(参考公式:当椭圆的长半轴长为a,短半轴长为b时,椭圆围成的区域的面积为 abπ)( )
内的概率(参考公式:当椭圆的长半轴长为a,短半轴长为b时,椭圆围成的区域的面积为 abπ)( )


