题目内容
 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠ABC=45°.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=2,∠ABC=45°.
(1)求点A 到平面 A1BC的距离;
(2)求二面角A-A1C-B的大小.
解:(1)∵AB=AC=2,∠ABC=45°,∴∠BAC=90°.
∴ =
= .
.
在直三棱柱ABC-A1B1C1中,∴A1A⊥AB,A1A⊥AC.
∴ .∴
.∴ =
= .
.
设点A到平面距离为h,由 =
= ,∴
,∴ ,解得
,解得 .
.
∴点A到平面距离为 .
.
(2)设A1C的中点为M,连接BM,AM.
∵BA1=BC,AA1=AC,∴BM⊥A1C,AM⊥A1C.
∴∠AMB是二面角A-A1C-B的平面角.
∵ ,∴
,∴ .
.
∴二面角A-A1C-B的大小为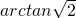 .
.
分析:(1)利用三棱锥的体积计算公式和等积变形即可得出;
(2)利用直角三角形斜边中线的性质和二面角的定义即可得出.
点评:熟练掌握三棱锥的体积计算公式、等积变形、直角三角形斜边中线的性质和二面角的定义是解题的关键.
∴
 =
= .
.
在直三棱柱ABC-A1B1C1中,∴A1A⊥AB,A1A⊥AC.
∴
 .∴
.∴ =
= .
.设点A到平面距离为h,由
 =
= ,∴
,∴ ,解得
,解得 .
.∴点A到平面距离为
 .
.(2)设A1C的中点为M,连接BM,AM.
∵BA1=BC,AA1=AC,∴BM⊥A1C,AM⊥A1C.
∴∠AMB是二面角A-A1C-B的平面角.
∵
 ,∴
,∴ .
.∴二面角A-A1C-B的大小为
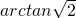 .
.分析:(1)利用三棱锥的体积计算公式和等积变形即可得出;
(2)利用直角三角形斜边中线的性质和二面角的定义即可得出.
点评:熟练掌握三棱锥的体积计算公式、等积变形、直角三角形斜边中线的性质和二面角的定义是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.