题目内容
3.已知函数f(x)=2x+1,x∈[1,4],求f(2x-1)的解析式.分析 求出所求函数的定义域,然后求出函数的解析式.
解答 解:x∈[1,4],则2x-1∈[1,4],可得:x∈[1,$\frac{5}{2}$].
函数f(x)=2x+1,x∈[1,4],
f(2x-1)=2(2x-1)+1=4x-1.
f(2x-1)的解析式为:g(x)=4x-1,x∈[1,$\frac{5}{2}$].
点评 本题考查函数的解析式的求法,注意函数的定义域.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.条件p:x1是方程f(x)=0的一个根,或x1是方程g(x)=0的一个根;条件q:x1是方程f(x)•g(x)=0的一个根.则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
16.已知x,y是正数,且xy=4,则$\frac{y}{\sqrt{x}}$+$\frac{x}{\sqrt{y}}$取得最小值时,x的值是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
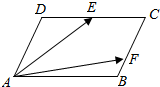 如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.
如图,平行四边形ABCD中,E为CD中点,F在线段BC上,且BC=3BF.已知$\overrightarrow{AD}$=x$\overrightarrow{AE}$+y$\overrightarrow{AF}$,则x的值为$\frac{6}{5}$.