题目内容
数列{an}为等差数列，an为正整数，其前n项和为Sn，数列{bn}为等比数列，且a1=3，b1=1，数列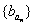
是公比为64的等比数列，b2S2=64，
（1）求an，bn；
（2）求证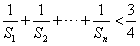
。
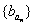是公比为64的等比数列，b2S2=64，（1）求an，bn；
（2）求证
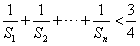。解：（1）设{an}的公差为d，{bn}的公比为q，则d为正整数，
，
依题意有
，①
由
知q为正有理数，故d为6的因子1，2，3，6之一，
解①得d=2，q=8，
故
。
（2）
，
∴
。
，依题意有
，① 由
知q为正有理数，故d为6的因子1，2，3，6之一，解①得d=2，q=8，
故
。（2）
，∴
。
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目