题目内容
(2012•河北模拟)如图,矩形ABCD中,AB=3,BC=4.E,F分别在线段BC和AD上,EF∥AB,将矩形ABEF沿EF折起.记折起后的矩形为MNEF,且平面MNEF⊥平面ECDF.

(Ⅰ)求证:NC∥平面MFD;
(Ⅱ)若EC=3,求证:ND⊥FC;
(Ⅲ)求四面体NFEC体积的最大值.

(Ⅰ)求证:NC∥平面MFD;
(Ⅱ)若EC=3,求证:ND⊥FC;
(Ⅲ)求四面体NFEC体积的最大值.
分析:(Ⅰ)先证明四边形MNCD是平行四边形,利用线面平行的判定,可证NC∥平面MFD;
(Ⅱ)连接ED,设ED∩FC=O.根据平面MNEF⊥平面ECDF,且NE⊥EF,可证NE⊥平面ECDF,从而可得FC⊥NE,进一步可证FC⊥平面NED,利用线面垂直的判定,可得ND⊥FC;
(Ⅲ)先表示出四面体NFEC的体积,再利用基本不等式,即可求得四面体NFEC的体积最大值.
(Ⅱ)连接ED,设ED∩FC=O.根据平面MNEF⊥平面ECDF,且NE⊥EF,可证NE⊥平面ECDF,从而可得FC⊥NE,进一步可证FC⊥平面NED,利用线面垂直的判定,可得ND⊥FC;
(Ⅲ)先表示出四面体NFEC的体积,再利用基本不等式,即可求得四面体NFEC的体积最大值.
解答: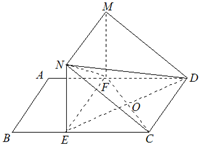 (Ⅰ)证明:因为四边形MNEF,EFDC都是矩形,
(Ⅰ)证明:因为四边形MNEF,EFDC都是矩形,
所以MN∥EF∥CD,MN=EF=CD.
所以四边形MNCD是平行四边形,…(2分)
所以NC∥MD,…(3分)
因为NC?平面MFD,所以NC∥平面MFD. …(4分)
(Ⅱ)证明:连接ED,设ED∩FC=O.
因为平面MNEF⊥平面ECDF,且NE⊥EF,
所以NE⊥平面ECDF,…(5分)
因为FC?平面ECDF,
所以FC⊥NE. …(6分)
又EC=CD,所以四边形ECDF为正方形,所以 FC⊥ED. …(7分)
所以FC⊥平面NED,…(8分)
因为ND?平面NED,
所以ND⊥FC. …(9分)
(Ⅲ)解:设NE=x,则EC=4-x,其中0<x<4.
由(Ⅰ)得NE⊥平面FEC,所以四面体NFEC的体积为VNFEC=
S△EFC•NE=
x(4-x). …(11分)
所以VNFEC≤
[
]2=2. …(13分)
当且仅当x=4-x,即x=2时,四面体NFEC的体积最大. …(14分)
 (Ⅰ)证明:因为四边形MNEF,EFDC都是矩形,
(Ⅰ)证明:因为四边形MNEF,EFDC都是矩形,所以MN∥EF∥CD,MN=EF=CD.
所以四边形MNCD是平行四边形,…(2分)
所以NC∥MD,…(3分)
因为NC?平面MFD,所以NC∥平面MFD. …(4分)
(Ⅱ)证明:连接ED,设ED∩FC=O.
因为平面MNEF⊥平面ECDF,且NE⊥EF,
所以NE⊥平面ECDF,…(5分)
因为FC?平面ECDF,
所以FC⊥NE. …(6分)
又EC=CD,所以四边形ECDF为正方形,所以 FC⊥ED. …(7分)
所以FC⊥平面NED,…(8分)
因为ND?平面NED,
所以ND⊥FC. …(9分)
(Ⅲ)解:设NE=x,则EC=4-x,其中0<x<4.
由(Ⅰ)得NE⊥平面FEC,所以四面体NFEC的体积为VNFEC=
| 1 |
| 3 |
| 1 |
| 2 |
所以VNFEC≤
| 1 |
| 2 |
| x+(4-x) |
| 2 |
当且仅当x=4-x,即x=2时,四面体NFEC的体积最大. …(14分)
点评:本题考查线面平行,考查线面垂直,考查三棱锥体积的计算,考查基本不等式的运用,掌握线面平行,线面垂直的判定方法,正确表示四面体NFEC的体积是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 (2012•河北模拟)设全集U=R,A={x|
(2012•河北模拟)设全集U=R,A={x| (2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是
(2012•河北模拟)如图是一个程序框图,该程序框图输出的结果是 (2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )
(2012•河北模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),其导函数f'(x)的部分图象如图所示,则函数f(x)的解析式为( )