题目内容
方程 的一个解是 ( )
的一个解是 ( )
| A.4 | B.3 | C.2 | D.1 |
C
解析本题是记忆联想题
看到3,4,5,联想勾股定理“勾三,股四,弦五”,所以 是
是 的一个解。故选择C
的一个解。故选择C

练习册系列答案
相关题目
函数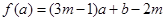 ,当
,当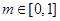 时,
时,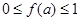 恒成立,则
恒成立,则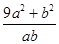
的最大值与最小值之和为 ( )
| A. 18 | B. 16 | C. 14 | D.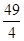 |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)(f(x2)-f(x1))>0,则当n∈N*时,有
( )
| A.f(-n)<f(n-1)<f(n+1) |
| B.f(n-1)<f(-n)<f(n+1) |
| C.f(n+1)<f(-n)<f(n-1) |
| D.f(n+1)<f(n-1)<f(-n) |
设函数 ,则
,则
A. | B. | C. | D. |
已知0< x<1,函数f ( x )=" x" (1-x ) 的最大值是( )
A. | B. | C.- | D.无最大值 |
.已知定义在R上的奇函数f(x),满足f(x-4)=-f(x),且在区间[0,2]上是增函数,
则
| A.f(33)<f(50)<f(-25) | B.f(50)<f(33)<f(-25) |
C.f (-25)<f(33)<f(50) (-25)<f(33)<f(50) | D.f(-25)<f(50)<f(33) |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
、已知定义域为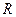 的函数
的函数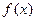 为偶函数,且当
为偶函数,且当 时,
时,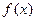 是减函数,设
是减函数,设
 ,
, ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
已知
 ,猜想
,猜想 的表达式( )
的表达式( )
A. ; ; | B. ; ; | C. ; ; | D. . . |