Question

求函数y=的定义域.

Answer 1

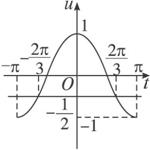
解法一:令3x=t,作出u=cost在一个周期［-π,π］内的图象如右图,可知使u≥-的t的范围为-≤t≤,∴2kπ-≤3x≤2kπ+,k∈Z,得定义域为{x|-≤x≤+,k∈Z}.

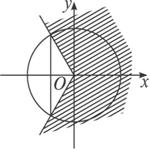
解法二:由1+2cos3x≥0,得cos3x≥-,如右图,在单位圆中作出余弦函数值等于-的两个角-、,故2kπ-≤3x≤2kπ+,k∈Z,

∴-≤x≤+,k∈Z,所以定义域为{x|-≤x≤+,k∈Z}.