题目内容
设函数 .
.
(Ⅰ)证明: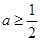 时,函数
时,函数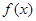 在
在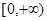 上单调递增;
上单调递增;
(Ⅱ)证明: .
.
【答案】
(Ⅰ)详见解析;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)导数法,令 ,
, ,再由
,再由 得出
得出 ,从而得出结论;(Ⅱ)用分析法证明,要证
,从而得出结论;(Ⅱ)用分析法证明,要证 ,只需证
,只需证 ,接着
,接着
构造新函数,用导数法求解.
试题解析:(Ⅰ)证明: ,则
,则 ,
, ,
,
∵ ,
, ,
,
∴ .
(3分)
.
(3分)
∴ 在
在 单调递增 ∴
单调递增 ∴ ,即
,即 ,
,
从而 在
在 上单调递增;.
(7分)
上单调递增;.
(7分)
(Ⅱ)证明:要证 ,
,
只需证 ,即
,即 ,证明如下:
,证明如下:
设 ,则
,则 ,(9分)
,(9分)
已知当 时,
时, ,
, 单调递减;
单调递减;
当 时,
时, ,
, 单调递增.
单调递增.
∴ 在
在 上的最小值为
上的最小值为 ,即
,即 , (12分)
, (12分)
又由(Ⅰ),当 且
且 时,
时, ,
,
∴ ,即不等式
,即不等式 恒成立. (14分)
恒成立. (14分)
考点:导数法求解函数的单调性,最值, 构造法.

练习册系列答案
相关题目

 证明:
证明: 。
。 对于
对于 及
及 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 .
. 图象的一个对称中心.
图象的一个对称中心. .
. 图象的一个对称中心.
图象的一个对称中心. .
.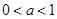 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件; 时,满足
时,满足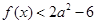 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, 是R上的增函数;(6分)
是R上的增函数;(6分) ;(4分)
;(4分) 。(4分)
。(4分)