题目内容
下列函数中,在其定义域内既是奇函数又是增函数的是( )
| A、y=-x2+5(x∈R) | ||
| B、y=-x3+x(x∈R) | ||
| C、y=x3(x∈R) | ||
D、y=-
|
分析:通过偶函数的定义判断出A不正确;通过对函数求导,令导数小于0,不等式有解,判断出B不正确;通过奇函数的定义及通过对函数求导数,判断出导函数的符号,判断出C正确;通过函数的单调性,判断出D不正确.
解答:解:对于A,y=-x2+5是偶函数
对于B,函数是奇函数,但y′=-3x2+1<0时x>
或x<-
所以函数在(
,+∞)和(-∞,-
上单减
故B错
对于C,y=x3是奇函数,且y′=3x2≥0恒成立,所以函数在定义域内是增函数,故C正确
对于D是奇函数,,但函数在(-∞,0)和(0,+∞)上是增函数,但在整个定义域上不是增函数
故选C.
对于B,函数是奇函数,但y′=-3x2+1<0时x>
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
故B错
对于C,y=x3是奇函数,且y′=3x2≥0恒成立,所以函数在定义域内是增函数,故C正确
对于D是奇函数,,但函数在(-∞,0)和(0,+∞)上是增函数,但在整个定义域上不是增函数
故选C.
点评:判断函数的奇偶性用的方法是定义法;判断函数的单调性常用导数.

练习册系列答案
相关题目
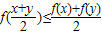 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数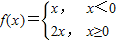
 ,则称这个函数是下凸函数,下列函数
,则称这个函数是下凸函数,下列函数