Question

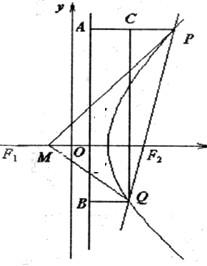
已知F₁（-2，0），F₂（2，0），动点P满足|PF₁|-|PF₂|=2，记动点P的轨迹为S，过点F₂作直线l与轨迹S交于P、Q两点，过P、Q作直线x=的垂线PA、QB，垂足分别为A、B，记λ=|AP|•|BQ|．
（Ⅰ）求轨迹S的方程；
（Ⅱ）设点M（-1，0），求证：当λ取最小值时，△PMQ的面积为9．

Answer 1

（Ⅰ）解：由|PF₁|-|PF₂|=2＜|F₁F₂|知，点P的轨迹S是以F₁、F₂为焦点的双曲线右支．…（1分）
由c=2，2a=2，∴b²=3． …（3分）
故轨迹S的方程为x²-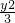=1 （x≥1）…（5分）
（Ⅱ）证明：当直线l的斜率存在时，…（6分）
设直线方程为y=k（x-2），P（x₁，y₁），Q（x₂，y₂），与双曲线方程联立消y得（k²-3）x²-4k²x+4k²+3=0 …（7分）
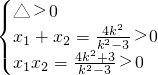∴解得k²＞3．…（9分）
∵λ=|AP|•|BQ|=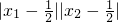=（2x₁-1）（2x₂-1）=[4x₁x₂-2（x₁+x₂）+1]=x₁x₂-+ …（11分）
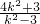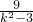=-+=+=+＞． …（12分）
当斜率不存在时，|AP|•|BQ|=，∴λ的最小值为．…（13分）
此时，|PQ|=6，|MF₂|=3，S_△PMQ=||MF₂|•|PQ|=9．…（14分）
分析：（Ⅰ）由|PF₁|-|PF₂|=2＜|F₁F₂|知，点P的轨迹S是以F₁、F₂为焦点的双曲线右支，结合焦点坐标，可求轨迹S的方程；（Ⅱ）当直线l的斜率存在时，设直线方程为y=k（x-2），与双曲线方程联立消y得（k²-3）x²-4k²x+4k²+3=0，结合韦达定理，及λ=|AP|•|BQ|，考虑直线斜率不存在，确定λ的最小值为，从而可求△PMQ的面积．
点评：本题考查双曲线的标准方程，考查双曲线的定义，考查直线与双曲线的位置关系，考查三角形面积的计算，属于中档题．