题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2,b=2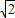 .
.(1)若∠C=45°,求c的值;
(2)若∠A=30°,求∠B的值.
【答案】分析:(1)利用余弦定理列出关系式,将a,b及cosC代入计算,即可求出c的值;
(2)由a,b,sinA的值,利用正弦定理求出sinB的值,再利用特殊角的三角函数值即可求出B的度数.
解答:解:(1)由余弦定理c2=a2+b2-2abcosC,得c2=22+(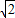 )2-2×2×2
)2-2×2×2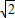 ×
×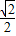 =4,
=4,
∴c=2;
(2)由正弦定理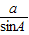 =
=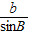 ,得sinB=
,得sinB=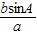 =
=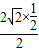 =
=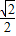 ,
,
∴∠B=45°或∠B=135°.
点评:此题考查了正弦定理、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.
(2)由a,b,sinA的值,利用正弦定理求出sinB的值,再利用特殊角的三角函数值即可求出B的度数.
解答:解:(1)由余弦定理c2=a2+b2-2abcosC,得c2=22+(
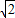 )2-2×2×2
)2-2×2×2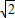 ×
×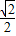 =4,
=4,∴c=2;
(2)由正弦定理
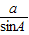 =
=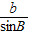 ,得sinB=
,得sinB=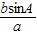 =
=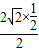 =
=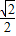 ,
,∴∠B=45°或∠B=135°.
点评:此题考查了正弦定理、余弦定理,以及特殊角的三角函数值,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |