题目内容
已知函数f(x)=lnx+ +x(a∈R).
+x(a∈R).
(1)求函数f(x)的单调区间;
(2)若以函数y=f(x)-x(0<x≤3)图象上任意一点P(x0,y0)为切点的切线的斜率k≤ 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.
(1)f(x)=lnx+ +x(x>0),f′(x)=
+x(x>0),f′(x)= -
- +1=
+1=
方程x2+x-a=0的判别式△=1+4a,
当a≤- 时,△≤0,f′(x)≥0,f(x)在(0,+∞)单调递增,
时,△≤0,f′(x)≥0,f(x)在(0,+∞)单调递增,
当- <a≤0时,△>0,方程x2+x-a=0有两个根均小于等于零;
<a≤0时,△>0,方程x2+x-a=0有两个根均小于等于零;
∴f′(x)≥0,f(x)在(0,+∞)单调递增,
当a>0时,,△>0,方程x2+x-a=0有一个正根 ,f(x)在(0,
,f(x)在(0, )单调递减,在(
)单调递减,在( ,+∞)单调递增
,+∞)单调递增
综上当a≤0时,f(x)在(0,+∞)单调递增;当a>0时,f(x)在(0, )单调递减,在(
)单调递减,在( ,+∞)单调递增
,+∞)单调递增
(2)y′=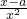 (0<x≤3),k=y′
(0<x≤3),k=y′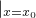 =
= ≤
≤ (0<x0≤3)恒成立?a≥
(0<x0≤3)恒成立?a≥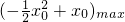 ,
,
当x0=1时, 取得最大值
取得最大值
∴a≥ ,
,
∴amin= .
.
分析:(1)f′(x)= ,方程x2+x-a=0的判别式△=1+4a,对△分△≤0与△>0两类讨论即可求得函数f(x)的单调区间;
,方程x2+x-a=0的判别式△=1+4a,对△分△≤0与△>0两类讨论即可求得函数f(x)的单调区间;
(2)k=y′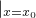 =
= ≤
≤ (0<x0≤3)恒成立?a≥
(0<x0≤3)恒成立?a≥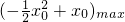 ,由二次函数的性质可得当x0=1时,
,由二次函数的性质可得当x0=1时, 取得最大值,问题得到解决.
取得最大值,问题得到解决.
点评:本题考查利用导数研究函数的单调性,考查函数恒成立问题,考查分类讨论思想与化归思想的综合运用,属于难题.
 +x(x>0),f′(x)=
+x(x>0),f′(x)= -
- +1=
+1=
方程x2+x-a=0的判别式△=1+4a,
当a≤-
 时,△≤0,f′(x)≥0,f(x)在(0,+∞)单调递增,
时,△≤0,f′(x)≥0,f(x)在(0,+∞)单调递增,当-
 <a≤0时,△>0,方程x2+x-a=0有两个根均小于等于零;
<a≤0时,△>0,方程x2+x-a=0有两个根均小于等于零;∴f′(x)≥0,f(x)在(0,+∞)单调递增,
当a>0时,,△>0,方程x2+x-a=0有一个正根
 ,f(x)在(0,
,f(x)在(0, )单调递减,在(
)单调递减,在( ,+∞)单调递增
,+∞)单调递增 综上当a≤0时,f(x)在(0,+∞)单调递增;当a>0时,f(x)在(0,
 )单调递减,在(
)单调递减,在( ,+∞)单调递增
,+∞)单调递增(2)y′=
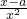 (0<x≤3),k=y′
(0<x≤3),k=y′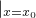 =
= ≤
≤ (0<x0≤3)恒成立?a≥
(0<x0≤3)恒成立?a≥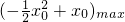 ,
,当x0=1时,
 取得最大值
取得最大值
∴a≥
 ,
,∴amin=
 .
.分析:(1)f′(x)=
 ,方程x2+x-a=0的判别式△=1+4a,对△分△≤0与△>0两类讨论即可求得函数f(x)的单调区间;
,方程x2+x-a=0的判别式△=1+4a,对△分△≤0与△>0两类讨论即可求得函数f(x)的单调区间;(2)k=y′
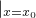 =
= ≤
≤ (0<x0≤3)恒成立?a≥
(0<x0≤3)恒成立?a≥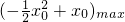 ,由二次函数的性质可得当x0=1时,
,由二次函数的性质可得当x0=1时, 取得最大值,问题得到解决.
取得最大值,问题得到解决.点评:本题考查利用导数研究函数的单调性,考查函数恒成立问题,考查分类讨论思想与化归思想的综合运用,属于难题.

练习册系列答案
相关题目