题目内容
函数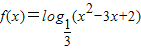 的单调递增区间为( )
的单调递增区间为( )A.(-∞,1)
B.(2,+∞)
C.(-∞,
 )
)D.(
 ,+∞)
,+∞)
【答案】分析:本题是一个复合函数,外层是一个递减的对数函数故求出函数的定义域以及内层函数的单调区间,依据复合函数的单调性判断规则做出判断求出内层函数的增区间即为复合函数的递增区间,从而找出正确选项即可.
解答:解:由题意,此复合函数,外层是一个递减的对数函数
令t=x2-3x+2>0解得x>2或x<1
由二次函数的性质知,t在(-∞,1)是减函数,在(2,+∞)上是增函数,
由复合函数的单调性判断知函数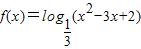 的单调递增区间(-∞,1)
的单调递增区间(-∞,1)
故选A
点评:本题考查用复合函数的单调性求单调区间,此题外层是一对数函数,故要先解出函数的定义域,在定义域上研究函数的单调区间,这是本题易失分点,切记!
解答:解:由题意,此复合函数,外层是一个递减的对数函数
令t=x2-3x+2>0解得x>2或x<1
由二次函数的性质知,t在(-∞,1)是减函数,在(2,+∞)上是增函数,
由复合函数的单调性判断知函数
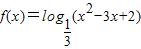 的单调递增区间(-∞,1)
的单调递增区间(-∞,1)故选A
点评:本题考查用复合函数的单调性求单调区间,此题外层是一对数函数,故要先解出函数的定义域,在定义域上研究函数的单调区间,这是本题易失分点,切记!

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 的单调递增区间为________________
的单调递增区间为________________ 的单调递增区间为
。
的单调递增区间为
。