题目内容
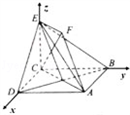
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=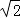 ,CE=EF=1.
,CE=EF=1.
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A﹣BE﹣D的大小 .
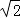 ,CE=EF=1.
,CE=EF=1.(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A﹣BE﹣D的大小 .
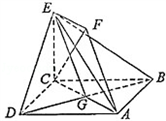
解:证明:(I)设AC与BD交于点G,因为EF∥AG,且EF=1,AG= AC=1,
AC=1,
所以四边形AGEF为平行四边形.所以AF∥EG.
因为EG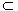 P平面BDE,AF
P平面BDE,AF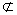 平面BDE,
平面BDE,
所以AF∥平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,
且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系C﹣xyz.
则C(0,0,0),A(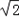 ,
,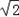 ,0),D(
,0),D(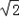 ,0,0),
,0,0),
E(0,0,1),F(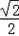 ,
,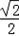 ,1).
,1).
所以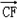 =(
=(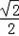 ,
,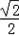 ,1),
,1),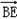 =(0,﹣
=(0,﹣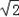 ,1),
,1),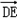 =(﹣
=(﹣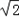 ,0,1).
,0,1).
所以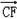
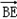 =0﹣1+1=0,
=0﹣1+1=0,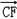
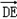 =﹣1+0+1=0.
=﹣1+0+1=0.
所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,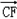 =(
=(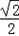 ,
,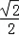 ,1),是平面BDE的一个法向量,
,1),是平面BDE的一个法向量,
设平面ABE的法向量 =(x,y,z),则
=(x,y,z),则
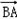 =0,
=0,
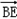 =0.即
=0.即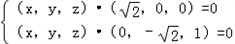
所以x=0,且z=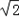 y.令y=1,则z=
y.令y=1,则z=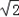 .
.
所以n=(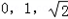 ),从而cos(
),从而cos( ,
,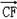 )=
)=
因为二面角A﹣BE﹣D为锐角,所以二面角A﹣BE﹣D为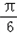 .
.
 AC=1,
AC=1,所以四边形AGEF为平行四边形.所以AF∥EG.
因为EG
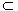 P平面BDE,AF
P平面BDE,AF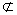 平面BDE,
平面BDE,所以AF∥平面BDE.
(II)因为正方形ABCD和四边形ACEF所在的平面互相垂直,
且CE⊥AC,所以CE⊥AC,所以CE⊥平面ABCD.
如图,以C为原点,建立空间直角坐标系C﹣xyz.
则C(0,0,0),A(
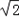 ,
,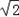 ,0),D(
,0),D(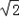 ,0,0),
,0,0),E(0,0,1),F(
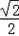 ,
,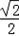 ,1).
,1).所以
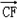 =(
=(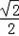 ,
,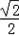 ,1),
,1),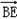 =(0,﹣
=(0,﹣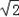 ,1),
,1),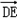 =(﹣
=(﹣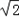 ,0,1).
,0,1).所以
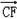
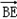 =0﹣1+1=0,
=0﹣1+1=0,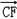
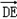 =﹣1+0+1=0.
=﹣1+0+1=0.所以CF⊥BE,CF⊥DE,所以CF⊥平面BDE
(III)由(II)知,
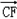 =(
=(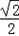 ,
,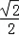 ,1),是平面BDE的一个法向量,
,1),是平面BDE的一个法向量,设平面ABE的法向量
 =(x,y,z),则
=(x,y,z),则
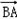 =0,
=0,
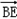 =0.即
=0.即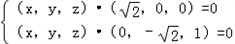
所以x=0,且z=
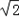 y.令y=1,则z=
y.令y=1,则z=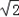 .
.所以n=(
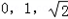 ),从而cos(
),从而cos( ,
,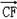 )=
)=
因为二面角A﹣BE﹣D为锐角,所以二面角A﹣BE﹣D为
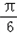 .
.

练习册系列答案
相关题目
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB= 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论: 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE. (2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为
(2010•温州二模)如图,正方形ABCD与正方形CDEF所成的二面角为60°,则直线EC与直线AD所成的角的余弦值为