题目内容
若直线mx+y-2m=0与直线（3m-4）x+y+1=0垂直，则m的值是（ ）
A．-1或
| B．1或
| C．-
| D．-
|
当m=0时，直线l1：y=0，斜率等于0，l2：-4x+y+1=0，不满足直线l1和直线l2垂直．
当两直线的斜率都存在时，由斜率之积等于-1可得-m•（4-3m）=-1，解得m=1或
，
综上得，m的值是 1 或
．
故选：B．
当两直线的斜率都存在时，由斜率之积等于-1可得-m•（4-3m）=-1，解得m=1或
| 1 |
| 3 |
综上得，m的值是 1 或
| 1 |
| 3 |
故选：B．
练习册系列答案
相关题目
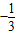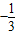或-1
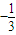或-1
或1
或-1
或1