题目内容
【题目】设等差数列![]() 的公差
的公差![]() ,前
,前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]()
(1)试寻找一个等差数列![]() 和一个非负常数
和一个非负常数![]() ,使得等式
,使得等式![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,并说明你的理由;
恒成立,并说明你的理由;
(2)对于(1)中的等差数列![]() 和非负常数
和非负常数![]() ,试求
,试求![]() (
(![]() )的最大值.
)的最大值.
【答案】(1)![]() ,详见解析(2)
,详见解析(2)![]()
【解析】
(1)由![]() ,
,![]() ,可得
,可得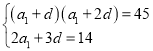 ,
,![]() ,解得
,解得![]() .可得
.可得![]() .由
.由![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,可得
恒成立,可得![]() .分别令
.分别令![]() ,及其
,及其![]() ,即可解得
,即可解得![]() .
.
(2)由(1)可得:![]() ,
,![]() ,
,![]() ,公差
,公差![]() .可得
.可得![]() .于是
.于是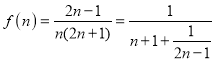 .令
.令![]() ,(
,(![]() ),利用导数研究其单调性最值即可得出.
),利用导数研究其单调性最值即可得出.
解:(1)![]()
![]() ,
,![]() ,
,
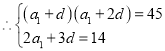 ,
,![]() ,
,
解得![]() ,
,![]() .
.
![]() .
.
![]() .
.
![]()
![]() 对于任意的正整数
对于任意的正整数![]() 恒成立,
恒成立,
![]() .
.
分别令![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
可得![]() ,
,![]() ,
,![]() .
.
![]() 数列
数列![]() 是等差数列,
是等差数列,
![]() .
.
化为:![]() ,解得
,解得![]() 或
或![]() .
.
![]() ,
,
![]() .
.
(2)由(1)可得:![]() ,
,![]() ,
,![]() ,公差
,公差![]() .
.
![]() .
.
![]()
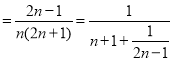 .
.
令![]() ,(
,(![]() ),
),
![]()
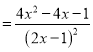
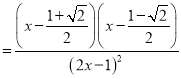 ,
,
可得: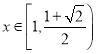 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
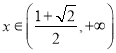 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
又![]() ,
,![]() .
.
因此当![]() 时,
时,![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
故![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目