题目内容
已知F是椭圆C1:
+
=1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.
(1)试判断以PF为直径的圆与圆C2的位置关系;
(2)在x轴上能否找到一定点M,使得
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(1)试判断以PF为直径的圆与圆C2的位置关系;
(2)在x轴上能否找到一定点M,使得
| QF |
| QM |
分析:(1)说明圆与圆的位置关系,只需说明其圆心距与半径之间的关系,由题意易得以PF为直径的圆与圆C2内切.
(2)先假设存在,转化为封闭型命题,从而有2(c-e2x)x0+e2a2+e2x2-a2-c2=0,要使其恒成立,必然有要c-e2x=0,从而问题得解.
(2)先假设存在,转化为封闭型命题,从而有2(c-e2x)x0+e2a2+e2x2-a2-c2=0,要使其恒成立,必然有要c-e2x=0,从而问题得解.
解答: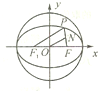 解:(1)取PF的中点记为N,椭圆的左焦点记为F1,连接ON,则ON为△PFF1的中位线,所以ON=
解:(1)取PF的中点记为N,椭圆的左焦点记为F1,连接ON,则ON为△PFF1的中位线,所以ON=
PF1.又由椭圆的定义可知,PF1+PF=2a,从而PF1=2a-PF,故ON=
PF1=
(2a-PF)=a-
PF.
所以以PF为直径的圆与圆C2内切.
(2)设椭圆的半焦距为c,M (x,0),Q (x0,y0),F (c,0),
由
=e,得QF2=e2QM2,即(x0-c)2+y02=e2[(x0-x)+y02].
把x02+y02=a2代入并化简整理,得2(c-e2x)x0+e2a2+e2x2-a2-c2=0,
要此方程对任意的Q (x0,y0)均成立,只要c-e2x=0即可,
此时x=
=
.所以x轴上存在点M,使得
=e,M的坐标为(
,0).
 解:(1)取PF的中点记为N,椭圆的左焦点记为F1,连接ON,则ON为△PFF1的中位线,所以ON=
解:(1)取PF的中点记为N,椭圆的左焦点记为F1,连接ON,则ON为△PFF1的中位线,所以ON=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以以PF为直径的圆与圆C2内切.
(2)设椭圆的半焦距为c,M (x,0),Q (x0,y0),F (c,0),
由
| QF |
| QM |
把x02+y02=a2代入并化简整理,得2(c-e2x)x0+e2a2+e2x2-a2-c2=0,
要此方程对任意的Q (x0,y0)均成立,只要c-e2x=0即可,
此时x=
| c |
| e2 |
| a2 |
| c |
| QF |
| QM |
| a2 |
| c |
点评:本题主要考查圆与圆的位置关系,考查椭圆的定义,对于存在性命题,通常是假设存在,从而转化为封闭型命题,以此为条件进行求解.

练习册系列答案
相关题目
 =1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.
=1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.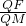 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由. =1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.
=1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点. =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.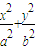 =1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.
=1的右焦点,点P是椭圆C1上的动点,点Q是圆C2:x2+y2=a2上的动点.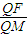 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.