题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c,且满足csinA=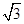 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )
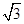 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )| A.1 | B.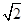 | C.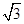 | D.3 |
C
由csinA=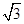 acosC,所以sinC sinA=
acosC,所以sinC sinA=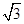 sinAcosC,即sinC =
sinAcosC,即sinC =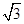 cosC,所以tanC=
cosC,所以tanC=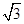 ,C=
,C= ,
,
A= -B,所以sinA+sinB=sin(
-B,所以sinA+sinB=sin( -B)+sinB=
-B)+sinB=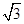 sin(B+
sin(B+ )∵0<B<
)∵0<B< ,∴
,∴ <B+
<B+ <
< ,∴sinA+sinB的最大值为
,∴sinA+sinB的最大值为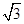 .故选C.
.故选C.
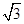 acosC,所以sinC sinA=
acosC,所以sinC sinA=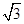 sinAcosC,即sinC =
sinAcosC,即sinC =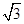 cosC,所以tanC=
cosC,所以tanC=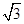 ,C=
,C= ,
,A=
 -B,所以sinA+sinB=sin(
-B,所以sinA+sinB=sin( -B)+sinB=
-B)+sinB=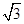 sin(B+
sin(B+ )∵0<B<
)∵0<B< ,∴
,∴ <B+
<B+ <
< ,∴sinA+sinB的最大值为
,∴sinA+sinB的最大值为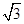 .故选C.
.故选C.
练习册系列答案
相关题目
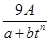 ,其中
,其中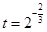 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 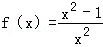 的定义域为E,值域为F.
的定义域为E,值域为F.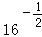 与集合F的关系;
与集合F的关系; },求实数a的值.
},求实数a的值.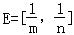 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.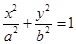 (a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q).
(a>b>0)的左焦为F,右顶点为A,上顶点为B,O为坐标原点,M为椭圆上任意一点,过F,B,A三点的圆的圆心为(p,q). 的最小值为
的最小值为 ,求椭圆的方程.
,求椭圆的方程.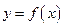 的图象与
的图象与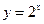 的图象关于直线
的图象关于直线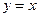 对称,则函数
对称,则函数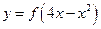 的递增区间是_________.
的递增区间是_________. 的图像如左图,则导函数
的图像如左图,则导函数 的图像可能是下图中的()
的图像可能是下图中的()

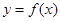 在
在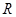 上为偶函数,当
上为偶函数,当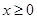 时,
时,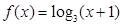 ,若
,若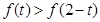 ,则实数
,则实数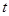 的取值范围是( )
的取值范围是( )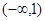
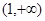
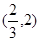
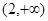
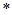 ”,对任意
”,对任意 ,
,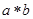 为唯一确定的实数,且具有性质:
为唯一确定的实数,且具有性质: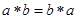 (2)对任意的
(2)对任意的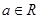 ,
,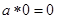 ;
;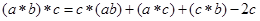
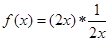 的性质,有如下说法:
的性质,有如下说法: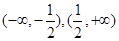 ,其中所有正确说法的个数( )
,其中所有正确说法的个数( )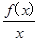 ,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.
,若函数h(x)在区间[1,2]上是增函数,求实数a的取值范围.