题目内容
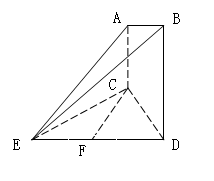
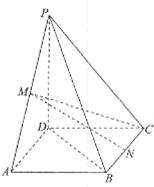
如图,在四棱锥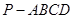 中,底面
中,底面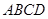 是矩形,
是矩形,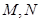 分别为
分别为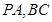 的中点,
的中点,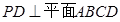 ,且
,且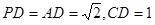
(1)证明: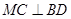 ;
;
(2)求二面角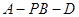 的余弦值。
的余弦值。
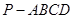 中,底面
中,底面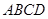 是矩形,
是矩形,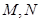 分别为
分别为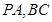 的中点,
的中点,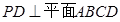 ,且
,且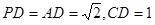

(1)证明:
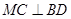 ;
;(2)求二面角
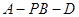 的余弦值。
的余弦值。(1)以D为坐标原点,射线DA,DC,DP分别为 轴、
轴、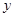 轴、
轴、 轴正半轴建立空间直角坐标系则D(0,0,0),A(
轴正半轴建立空间直角坐标系则D(0,0,0),A(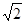 ,0,0),B(
,0,0),B(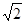 ,1,0)
,1,0)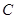 (0,1,0)P(0,0,
(0,1,0)P(0,0,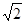 )
)
所以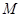 (
( ,0,
,0, ),
),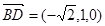 ,
,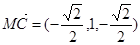 ∵
∵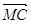 ·
·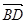 =0,所以MC⊥BD(2)
=0,所以MC⊥BD(2)
 轴、
轴、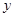 轴、
轴、 轴正半轴建立空间直角坐标系则D(0,0,0),A(
轴正半轴建立空间直角坐标系则D(0,0,0),A(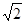 ,0,0),B(
,0,0),B(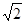 ,1,0)
,1,0)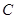 (0,1,0)P(0,0,
(0,1,0)P(0,0,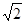 )
)所以
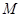 (
( ,0,
,0, ),
),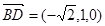 ,
,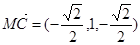 ∵
∵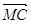 ·
·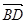 =0,所以MC⊥BD(2)
=0,所以MC⊥BD(2)
试题分析:(1)证明:因为PD⊥平面ABCD,
所以PD⊥DA,PD⊥DC,
在矩形ABCD中,AD⊥DC,
如图,以D为坐标原点,
射线DA,DC,DP分别为
 轴、
轴、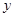 轴、
轴、 轴
轴正半轴建立空间直角坐标系 4分
则D(0,0,0),A(
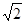 ,0,0),
,0,0),B(
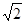 ,1,0)
,1,0)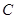 (0,1,0),
(0,1,0),P(0,0,
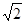 ) 6分
) 6分所以
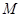 (
( ,0,
,0, ),
),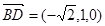 ,
,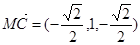 7分∵
7分∵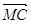 ·
·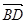 =0,所以MC⊥BD 7分
=0,所以MC⊥BD 7分(2)解:因为ME∥PD,所以ME⊥平面ABCD,ME⊥BD,又BD⊥MC,
所以BD⊥平面MCE,
所以CE⊥BD,又CE⊥PD,所以CE⊥平面PBD, 9分
由已知
 ,所以平面PBD的法向量
,所以平面PBD的法向量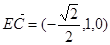 10分
10分M为等腰直角三角形PAD斜边中点,所以DM⊥PA,
又CD⊥平面PAD,AB∥CD,所以AB⊥平面PAD,AB⊥DM,
所以DM⊥平面PAB, 11分
所以平面PAB的法向量
 (-
(- ,0,
,0, ) 12分
) 12分设二面角A—PB—D的平面角为θ,
则
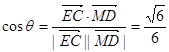 .
.所以,二面角A—PB—D的余弦值为
 . 15分
. 15分点评:本题中充分利用DA,DC,DP两两垂直建立空间直角坐标系,将证明两线垂直转化为两直线的法向量垂直,将求二面角转化为求两个平面的法向量的夹角

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
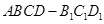 中,四边形
中,四边形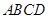 为菱形,
为菱形,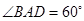 ,
,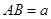 ,面
,面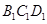 ∥面
∥面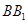 、
、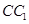 、
、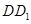 都垂直于面
都垂直于面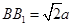 ,
,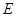 为
为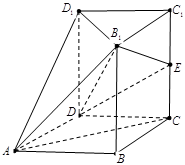
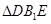 为等腰直角三角形;
为等腰直角三角形;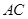 ∥面
∥面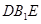 .
.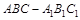 中,
中,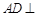 平面
平面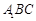 ,其垂足
,其垂足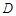 落在直线
落在直线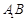 上.
上.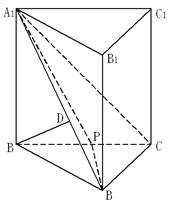
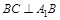 ;
;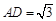 ,
,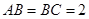 ,
,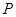 为
为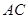 的中点,求三棱锥
的中点,求三棱锥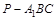 的体积.
的体积.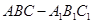 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,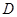 为
为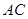 的中点.
的中点.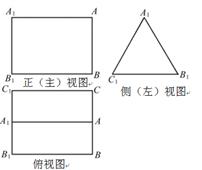
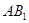 ∥平面
∥平面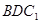 ;
;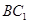 ,且
,且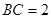 ,求点
,求点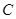 到平面
到平面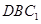 的距离.
的距离. 是半圆
是半圆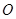 的直径,
的直径, 是半圆
是半圆 、
、 外的一个动点,
外的一个动点, 垂直于半圆
垂直于半圆 ,
, ,
, ,
, .
.
 平面
平面 ;
; 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值.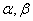 是两个不同的平面,
是两个不同的平面,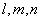 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是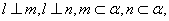 则
则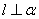
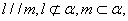 则
则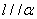
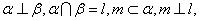 则
则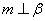
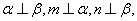 ,则
,则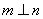
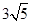 .
.
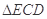 为等边三角形,F为ED边上的中点,且
为等边三角形,F为ED边上的中点,且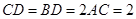 ,
,