Question

图11是一个正方体，H、G、F分别是棱AB、AD、AA₁的中点.现在沿△GFH所在平面锯掉正方体的一个角，问锯掉部分的体积是原正方体体积的几分之几?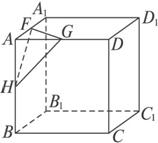

图11

Answer 1

分析:因为锯掉的是正方体的一个角，所以HA与AG、AF都垂直，即HA垂直于立方体的上底面.实际上锯掉的这个角，是以三角形AGF为底面，H为顶点的一个三棱锥.

解：设正方体的棱长为a，则正方体的体积为a³.

    三棱锥的底面是Rt△AGF，即∠FAG为90°，G、F又分别为AD、AA₁的中点，所以AF=AG=a.所以△AGF的面积为×a×a=8a².又因AH是三棱锥的高，H又是AB的中点，所以AH=a.所以锯掉的部分的体积为×a×a²=a³.

因为a³÷a³=,所以锯掉的那块的体积是原正方体体积的.