Question

【题目】设全集，关于的不等式（）的解集为.

（1）求集合；

（2）设集合，若 中有且只有三个元素，求实数的取值范围.

Answer 1

【答案】（1）当时，是；当时，；

（2）.

【解析】

（1）将不等式化简,结合绝对值的意义解不等式即可.

（2）讨论与两种情况下的情况.将集合B化简,结合正弦函数定义可求得集合B.再由 中有且只有三个元素可得关于的不等式组,解不等式即可求得的取值范围.

（1）由

化简可得

当时,解集是；

当时, 或

解得或

所以解集是或

综上所述, 当时,解集是；当时, 解集是或

（2）(i)当时, ,不合题意；

(ii)当时, 。

结合正弦的差角公式与余弦的差角公式展开化简可得

,

由正弦函数的性质,

得,即,所以

当有3个元素时,

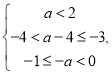满足或

解不等式组可得，