题目内容
求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-3=0和x2+y2-4y-3=0的交点的圆的方程.
解:画出如图4-2-7,设经过两已知圆的交点的圆的方程为x2+y2-4x-3+λ(x2+y2-4y-3)=0,
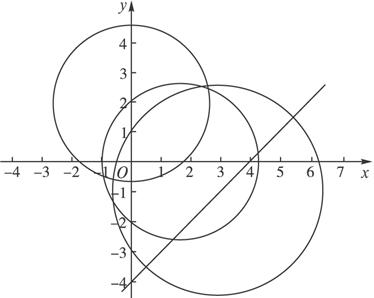
图4-2-7
则其圆心坐标为(
).∵所求圆的圆心在直线x-y-4=0上,
∴
-4=0,解得λ=
.
∴所求圆的方程为x2+y2-6x+2y-3=0.
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-3=0和x2+y2-4y-3=0的交点的圆的方程.
解:画出如图4-2-7,设经过两已知圆的交点的圆的方程为x2+y2-4x-3+λ(x2+y2-4y-3)=0,
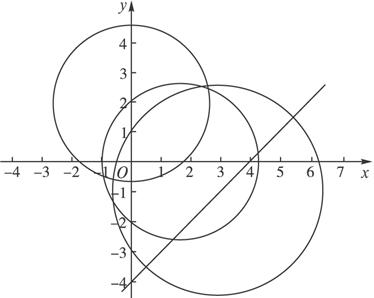
图4-2-7
则其圆心坐标为().∵所求圆的圆心在直线x-y-4=0上,
∴-4=0,解得λ=.
∴所求圆的方程为x2+y2-6x+2y-3=0.
名校课堂系列答案