题目内容
已知平面内两点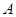
（-1,1），
（1,3）.
(Ⅰ)求过
两点的直线方程；
(Ⅱ)求过两点且圆心在
轴上的圆的方程.
(Ⅰ) 
；(Ⅱ) 
解析试题分析：(Ⅰ)可用两点式直接求直线方程，也可先求斜率再用点斜式求直线方程。(Ⅱ)可用直接法求圆心和半径，因为弦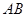
的中垂线过圆心，又因为圆心在轴上从而确定圆心，再用两点间距离公式求半径；还可以用待定系数法求圆的方程，本题设圆的标准方程较好，再根据已知条件3个列出方程，解方程组即可求出未知量，从而得圆的方程。
试题解析：解：(Ⅰ)
， 2分
所以直线的方程为
，
即.4分
(Ⅱ)因为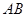的中点坐标为
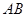，的中垂线为
，
又因为圆心在轴上，解
得圆心为
,6分
半径
, 8分
所以圆的方程为 .10分
考点：直线方程及圆的方程。
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
为参数），圆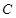
的极坐标方程为
.
对称，求
的值；
上的圆C.
轴相切时，求圆C的方程；
,求圆心的横坐标
的取值范围.
）两点，且圆心C在直线l：x-y+1=0上，求圆C的标准方程.
的圆心与点
关于直线
对称，直线
与圆
、
两点，且
，求圆
到定点
与到定点
的距离之比为
.
的轨迹C的方程，并指明曲线C的轨迹；
,若曲线C上恰有三个点到直线
的距离为1，求实数
的值。
，直线
．
与圆C的位置关系；
，求此时直线
在极坐标系中的方程为
，圆C在极坐标系中的方程为
，求圆C被直线