Question

如图2-3,D、E是△ABC的BC、AC两边上两点,且∠ADB=∠AEB.

求证:∠CED=∠ABC.

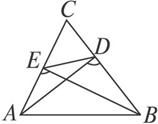
图2-3

Answer 1

思路分析:要证∠CED=∠ABC,容易想到圆内接四边形的性质.而证A、B、D、E四点共圆,用圆内接四边形判定定理不易找到条件,我们采用分类讨论思想.

证明:作△ABE的外接圆⊙O,则点D与⊙O有三种位置关系:①点D在圆外;②点D在圆内;③点D在圆上.

(1)如果点D在圆外,设BD与⊙O交于点F,连结AF,

则∠AFB=∠AEB,而∠AEB=∠ADB.

∴∠AFB=∠ADB.

这与“三角形的外角大于任一不相邻的内角”矛盾.

故点D不能在圆外.

(2)如果点D在圆内,设⊙O与CD交于F,连结AF,则∠AFB=∠AEB.

又∵∠AEB=∠ADB,∴∠AFB=∠ADB.

这也与“三角形的外角大于任一不相邻的内角”矛盾.

故点D不可能在圆内.

综上所求,A、B、D、E在同一圆上.∴∠CED=∠ABC.