题目内容
【题目】设抛物线![]() 上的点
上的点![]() 到焦点
到焦点![]() 的距离
的距离![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
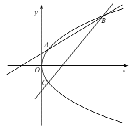
(Ⅱ)如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点是
轴的对称点是![]() .求证:直线
.求证:直线![]() 恒过一定点.
恒过一定点.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)先由抛物线定义用坐标表示![]() ,进而得
,进而得![]() ,再根据点在抛物线上,联立方程组可解出
,再根据点在抛物线上,联立方程组可解出![]() .(Ⅱ)证明直线过定点,一般方法为以算代证,即先求出直线方程,再将直线方程化为点斜式证明过定点.具体方法为先设
.(Ⅱ)证明直线过定点,一般方法为以算代证,即先求出直线方程,再将直线方程化为点斜式证明过定点.具体方法为先设![]() 两点(用纵坐标表示),根据直线
两点(用纵坐标表示),根据直线![]() 与抛物线位置关系得两点坐标关系
与抛物线位置关系得两点坐标关系![]() .再根据两点式写出直线
.再根据两点式写出直线![]() 方程,化成点斜式得定点(或令
方程,化成点斜式得定点(或令![]() 解得
解得![]() )
)
试题解析:解:(Ⅰ)由抛物线定义得![]()
又![]() ,所以
,所以![]() ,即
,即![]()
代入![]() ,得
,得![]() ,由
,由![]() 得
得![]() .
.
所以抛物线![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,联立直线与抛物线方程:
,联立直线与抛物线方程:
![]() ,
,
消去![]() 得
得![]() ,
,
由韦达定理可得![]() .
.
又由![]() ,可得直线
,可得直线![]() 的方程为:
的方程为:
![]() ,
,
∵![]() ,
,
∴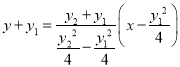 ,
,
即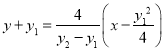 ,
,
![]() ,
,
∴![]() ,
,
∴直线![]() 恒过定点
恒过定点![]() .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目