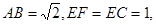题目内容
正方形ABCD在直角坐标平面内,已知一条边AB在直线y=x+4上,C、D在抛物线y2=x上,求正方形ABCD的面积.
解:设CD所在直线方程为y=x+b,C(x1,y1),D(x2,y2).
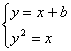
![]() x2+(2b-1)x+b2=0.
x2+(2b-1)x+b2=0.
x1+x2=1-2b,x1x2=b2.
∴|CD|=![]() =
=![]() =
=![]() .
.
又直线AB与CD间距离为|AD|=![]() ,
,
∵|AD|=|CD|,
∴![]() =
=![]() .
.
解得b=-6或b=-2.
从而所求边长为3![]() 或5
或5![]() .
.
SABCD=(3![]() )2=18或SABCD=(5
)2=18或SABCD=(5![]() )2=50.
)2=50.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
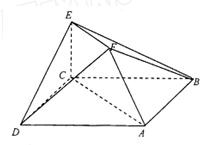 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=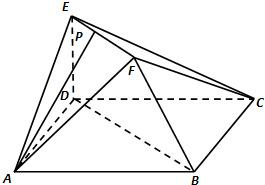 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=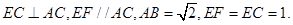
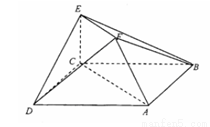
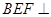 平面DEF;
平面DEF;