题目内容
已知a,x∈R,函数f(x)=sin2x-(2
+
a)sin(x+
)-
.
(1)设t=sinx+cosx,把函数f(x)表示为关于t的函数g(t),求g(t)表达式和定义域;
(2)对任意x∈[0,
],函数f(x)>-3-2a恒成立,求a的取值范围.
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(x-
|
(1)设t=sinx+cosx,把函数f(x)表示为关于t的函数g(t),求g(t)表达式和定义域;
(2)对任意x∈[0,
| π |
| 2 |
分析:(1)利用两角和的正弦公式可得t=sinx+cosx=
sin(x+
)∈[-
,
],把t=sinx+cosx两边平方化为sinxcosx=
.代入即可得到g(t)及其定义域;
(2))由x∈[0,
],可得t=sinx+cosx=
sin(x+
)∈[1,
],通过换元,由函数f(x)>-3-2a恒成立,分离参数即可得到a>
-
=t+
=p(t),
利用导数或单调性的定义即可得到p(t)的单调性和值域.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| t2-1 |
| 2 |
(2))由x∈[0,
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
| t2-2t |
| t-2 |
| 4-2t |
| t(t-2) |
| 2 |
| t |
利用导数或单调性的定义即可得到p(t)的单调性和值域.
解答:解:(1)∵t=sinx+cosx=
sin(x+
)∈[-
,
],
又t2=sin2x+cos2x+2sinxcosx,
∴sinxcosx=
.
∵f(x)=2sinxcosx-(2+a)(sinx+cosx)-
.
∴f(x)=g(t)=t2-(2+a)t-
-1,定义域:[-
,0)∪(0,
].
(2)∵x∈[0,
],∴t=sinx+cosx=
sin(x+
)∈[1,
],
∵函数f(x)>-3-2a恒成立,∴t2-(2+a)t-
-1>-3-2a恒成立,
得:t2-2t-
+2>(t-2)a,
∵t-2<0,∴a>
-
=t+
=p(t),
设1≤t1≤t2≤
,∵p(t2)-p(t1)=(t2-t1)(
)<0,
∴函数p(t)在[1,
]上是递减函数,
∴a>pmax(x)=p(1)=3.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
又t2=sin2x+cos2x+2sinxcosx,
∴sinxcosx=
| t2-1 |
| 2 |
∵f(x)=2sinxcosx-(2+a)(sinx+cosx)-
| 4 |
| sinx+cosx |
∴f(x)=g(t)=t2-(2+a)t-
| 4 |
| t |
| 2 |
| 2 |
(2)∵x∈[0,
| π |
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∵函数f(x)>-3-2a恒成立,∴t2-(2+a)t-
| 4 |
| t |
得:t2-2t-
| 4 |
| t |
∵t-2<0,∴a>
| t2-2t |
| t-2 |
| 4-2t |
| t(t-2) |
| 2 |
| t |
设1≤t1≤t2≤
| 2 |
| t1t2-2 |
| t1t2 |
∴函数p(t)在[1,
| 2 |
∴a>pmax(x)=p(1)=3.
点评:熟练掌握两角和的正弦公式、sinx+cosx与sinxcosx的关系、倍角公式、三角函数的单调性、单调性的定义、分离参数法是解题的关键.

练习册系列答案
相关题目
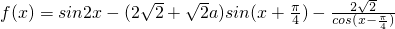 .
. ,函数f(x)>-3-2a恒成立,求a的取值范围.
,函数f(x)>-3-2a恒成立,求a的取值范围.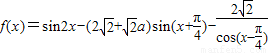 .
.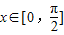 ,函数f(x)>-3-2a恒成立,求a的取值范围.
,函数f(x)>-3-2a恒成立,求a的取值范围.