题目内容
7．
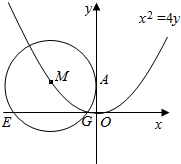设圆M过点A（0，2），且圆心M在曲线C：x2=4y上，EG是圆M在x轴上截得的弦，试探究当M运动时．弦长|EG|是否为定值？为什么？
分析 待定系数法设出圆的方程，设出圆与x轴的两个交点E，G的坐标，再由韦达定理和弦长公式，再根据圆心在抛物线上，将圆心坐标代入抛物线，两个式子联立可求出|x1-x2|是否为定值．
解答 解：设圆的圆心为M（a，b），
∵圆M过A（0，2），
∴圆的方程为 （x-a）2+（y-b）2=a2+（b-2）2，
令y=0得：x2-2ax+4b-4=0，
设圆与x轴的两交点分别为（x1，0），（x2，0），
x1+x2=2a，x1x2=4b-4，
|x1-x2|=$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{4{a}^{2}-16b+16}$，
又∵点M（a，b）在抛物线x2=4y上，
∴a2=4b，
∴$\sqrt{16b-16b+16}$=4，
即|EG|=4，
∴当M运动时，弦长|EG|为定值4．
点评 本题考查圆与抛物线相交关系的应用，考查了圆的定义，以及运算能力，属于中档题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目