题目内容
已知直线
⊥平面
，直线m
，给出下列命题：
①
∥
②
∥m; ③
∥m
④
∥
其中正确的命题是（ ）
A．①②③ B．②③④ C．②④ D．①③
【答案】
D
【解析】
试题分析：因为直线
⊥平面
，直线m
若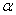
∥
成立，所以①正确.根据选项只要考虑选项②是否正确即可选出答案.若直线⊥平面，直线m则
∥m不成立，这个条件下直线
与直线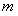
可能是相交、平行或异面三种位置关系.故选D.
考点：1.线面垂直、平行.3.面面垂直、平行.3.排除法的使用.
练习册系列答案
相关题目
已知直线
⊥平面α，直线
平面β，给出下列命题：
①α∥β
l⊥m ②α⊥βl∥m ③l∥m α⊥β ④l⊥mα∥β
其中正确命题的序号是 （ ）
| A．①②③ | B．②③④ | C．①③ | D．②④ |
有一段演绎推理是这样的：“直线平行于平面,则平行于平面内所有直线；已知直线
平面
，直线
平面，直线
∥平面，则直线∥直线
”的结论显然是错误的，这是因为（ ）
| A．大前提错误 | B．小前提错误 |
| C．推理形式错误 | D．非以上错误 |
平面
，直线
平面
∥平面
”的结论显然是错误的，这是因为（ ▲ ） 
平面
，直线
平面
平面
” ．结论显然