题目内容
把24粒种子分别种在8个坑内，每坑3粒，每粒种子发芽的概率为0.5，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑里的种子都没发芽，则这个坑需要补种，假定每个坑至多补种一次，每补种1个坑需10元，用ξ表示补种费用，则ξ的数学期望为（ ）
分析：一个坑里的3个种子发芽情况可以看做是3次独立重复试验，一个坑里的三颗种子都不发芽的概率是
，8个坑的补种情况可以看做是8次独立重复试验，设η代表补种次数，则η～B（8，
），由此能求出ξ的数学期望．
| 1 |
| 8 |
| 1 |
| 8 |
解答：解：一个坑里的3个种子发芽情况可以看做是3次独立重复试验，
可知一个坑里的三颗种子都不发芽的概率是
，
8个坑的补种情况可以看做是8次独立重复试验，
设η代表补种次数，则η～B（8，
），
∴Eη=np=8×
=1，
ξ=10η，所以Eξ=E（10η）=10，
所以ξ的数学期望为10元．
故选A．
可知一个坑里的三颗种子都不发芽的概率是
| 1 |
| 8 |
8个坑的补种情况可以看做是8次独立重复试验，
设η代表补种次数，则η～B（8，
| 1 |
| 8 |
∴Eη=np=8×
| 1 |
| 8 |
ξ=10η，所以Eξ=E（10η）=10，
所以ξ的数学期望为10元．
故选A．
点评：本题考查离散型随机变量的数学期望的求法，是基础题，解题时要认真审题，仔细解答，注意二项分布的合理运用．
练习册系列答案
相关题目
表示补种费用，则
，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑里的种子都没发芽，则这个坑需要补种，假定每个坑至多补种一次，每补种1个坑需10元，用
表示补种费用，则
，若一个坑内至少有1粒种子发芽，则这个坑不需要补种，若一个坑里的种子都没发芽，则这个坑需要补种，假定每个坑至多补种一次，每补种1个坑需10元，用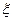
表示补种费用，则