题目内容
设{ }为等差数列,公差d = -2,
}为等差数列,公差d = -2, 为其前n项和.若
为其前n项和.若 ,则
,则 =
=
| A.18 | B.20 | C.22 | D.24 |
B
解析试题分析:由等差数列的前10项的和等于前11项的和可知,第11项的值为0,然后根据等差数列的通项公式,利用首项和公差d表示出第11项,让其等于0列出关于首项的方程,求出方程的解即可得到首项的值.解:由s10=s11,得到a1+a2+…+a10=a1+a2+…+a10+a11即a11=0,所以a1-2(11-1)=0,解得a1=20.故选B
考点:等差数列的性质
点评:此题考查学生掌握等差数列的性质,灵活运用等差数列的通项公式化简求值,是一道基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列 满足
满足 ,
, ,则
,则 ( )
( )
| A.121 | B.136 | C.144 | D.169 |
设数列 是等差数列,其前
是等差数列,其前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( )
| A.31 | B.32 | C.33 | D.34 |
在等差数列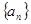 中,已知
中,已知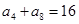 ,则
,则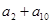 为 ( )
为 ( )
A.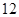 | B.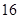 | C.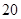 | D.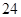 |
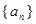 为等差数列,
为等差数列,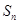 为其前
为其前 项和,
项和,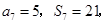 则
则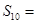
A.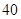 | B.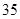 | C.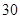 | D.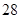 |
若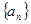 为等差数列,
为等差数列,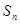 是其前n项的和,且
是其前n项的和,且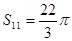 ,则
,则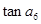 =( )
=( )
A.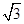 | B.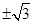 | C.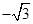 | D.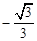 |
已知等差数列 中,
中, ,则
,则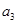 =( )
=( )
| A.10 | B.20 | C.30 | D.40 |
若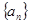 为等差数列,
为等差数列,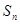 是其前
是其前 项的和,且
项的和,且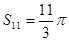 ,则
,则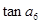 =( )
=( )
A.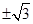 | B. | C.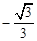 | D.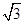 |
已知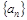 为等差数列,其前
为等差数列,其前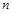 项和为
项和为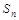 ,若
,若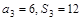 ,则公差
,则公差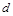 等于( )
等于( )
A.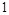 | B. | C.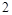 | D.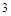 |