题目内容
如图，已知正方形ABCD的边长为3，E为DC的中点，AE与BD交于点F．则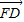
= ．
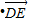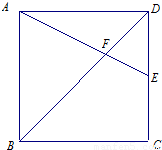
【答案】分析：由四边形ABCD是正方形，求得AE的长，再由△ABE∽△FDE，根据相似三角形的对应边成比例，求得EF的大小．再利用另个向量的数量积的定义求得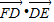
=
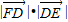cos（π-∠FDE）的值．
解答：解：：∵四边形ABCD是正方形，∴DE=
CD=
，∠ADE=90°，AB∥CD，∠FDE=45°．
∴AE=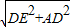
=
=
．
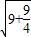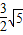∵AB∥CD，∴△ABF∽△EDF，
∴BF：DF=AB：DE=2，∴FD=
BD=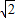
．
，
=
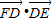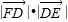cos（π-∠FDE）=
•
•（-
）=-
，
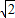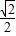故答案为-
．
点评：此题考查两个向量的数量积的定义，相似三角形的判定与性质、正方形的性质以及勾股定理，属于中档题．
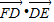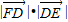=cos（π-∠FDE）的值．解答：解：：∵四边形ABCD是正方形，∴DE=
CD=，∠ADE=90°，AB∥CD，∠FDE=45°．∴AE=
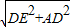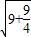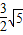==．∵AB∥CD，∴△ABF∽△EDF，
∴BF：DF=AB：DE=2，∴FD=
BD=．，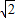
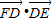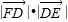=cos（π-∠FDE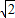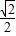）=••（-）=-，故答案为-
．点评：此题考查两个向量的数量积的定义，相似三角形的判定与性质、正方形的性质以及勾股定理，属于中档题．
练习册系列答案
相关题目
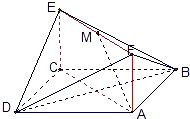如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
如图，已知正方形ABCD的边长为1，过正方形中心O的直线MN分别交正方形的边AB，CD于M，N，则当
如图，已知正方形ABCD和梯形ACEF所在平面互相垂直，AB=2，AF=
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，
（2012•深圳二模）如图，已知正方形ABCD在水平面上的正投影（投影线垂直于投影面）是四边形A′B′C′D′，其中A与A'重合，且BB′＜DD′＜CC′．