题目内容
函数f(x)的导函数为f′(x),若对于定义域内任意x1、x2(x1≠x2),有![]() 恒成立,则称f(x)为恒均变函数.给出下列函数:
恒成立,则称f(x)为恒均变函数.给出下列函数:
①f(x)=2x+3;
②f(x)=x2﹣2x+3;
③f(x)=![]() ;
;
④f(x)=ex;
⑤f(x)=lnx.
其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
考点:
导数的运算;命题的真假判断与应用.
专题:
计算题;新定义.
分析:
对于所给的每一个函数,分别计算![]() 和
和![]() 的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
解答:
解:对于①f(x)=2x+3,![]() =
=![]() =2,
=2,![]() =2,满足
=2,满足![]() ,为恒均变函数.
,为恒均变函数.
对于②f(x)=x2﹣2x+3,![]() =
=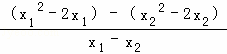 =
=![]() =x1+x2﹣2
=x1+x2﹣2
![]() =2•
=2•![]() ﹣2=x1+x2﹣2,故满足
﹣2=x1+x2﹣2,故满足![]() ,为恒均变函数.
,为恒均变函数.
对于;③![]() ,
,![]() =
=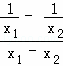 =
=![]() ,
,![]() =﹣
=﹣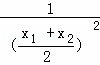 =
=![]() ,
,
显然不满足![]() ,故不是恒均变函数.
,故不是恒均变函数.
对于④f(x)=ex ,![]() =
=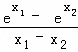 ,
,![]() =
=![]() ,显然不满足
,显然不满足
![]() ,故不是恒均变函数.
,故不是恒均变函数.
对于⑤f(x)=lnx,![]() =
=![]() =
=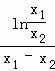 ,
,![]() =
=![]() ,
,
显然不满足 ![]() ,故不是恒均变函数.
,故不是恒均变函数.
故答案为 ①②.
点评:
本题主要考查函数的导数运算,“恒均变函数”的定义,判断命题的真假,属于基础题.

练习册系列答案
相关题目
 已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,
已知函数f(x)的定义域为[-2,+∞),部分对应值如下表,| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
| b+3 |
| a+3 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-
|
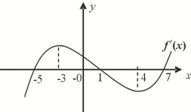 4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论:
4、已知函数f(x)的导函数的图象如图所示,给出下列四个结论: