题目内容
已知非零向量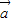 ,
,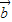 满足丨
满足丨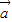 -
-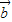 |=|
|=|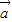 +
+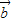 |=λ|
|=λ|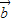 |(λ≥2),则向量
|(λ≥2),则向量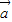 +
+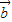 与
与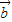 -
-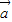 的夹角的最小值为 .
的夹角的最小值为 .
【答案】分析:由题意可得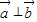 ,可得
,可得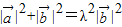 ,而cosθ=
,而cosθ=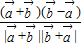 =
=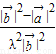 ,代入可得关于λ的式子,由已知的范围可求得其范围,进而可得答案.
,代入可得关于λ的式子,由已知的范围可求得其范围,进而可得答案.
解答:解:由丨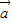 -
-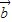 |=|
|=|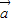 +
+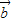 |平方可得
|平方可得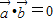 ,
,
即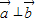 ,由向量的运算法则作出向量图,
,由向量的运算法则作出向量图,
由勾股定理可得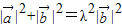 ,
,
设向量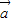 +
+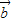 与
与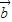 -
-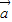 的夹角为θ,
的夹角为θ,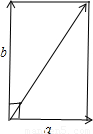
则cosθ=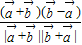 =
=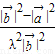
=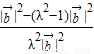 =
=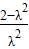 =
=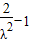 ,
,
∵λ≥2,∴λ2≥4,0<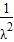
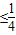 ,
,
∴-1<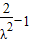
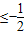 ,即-1<cosθ
,即-1<cosθ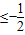 ,
,
又θ∈[0,π],所以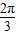 ≤θ≤π,
≤θ≤π,
故向量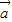 +
+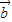 与
与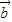 -
-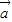 的夹角的最小值为
的夹角的最小值为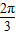
故答案为: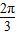
点评:本题考查数量积表示向量的夹角,涉及向量的模长和三角函数的取值范围,属中档题.
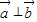 ,可得
,可得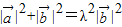 ,而cosθ=
,而cosθ=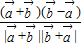 =
=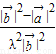 ,代入可得关于λ的式子,由已知的范围可求得其范围,进而可得答案.
,代入可得关于λ的式子,由已知的范围可求得其范围,进而可得答案.解答:解:由丨
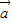 -
-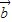 |=|
|=|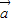 +
+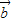 |平方可得
|平方可得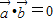 ,
,即
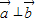 ,由向量的运算法则作出向量图,
,由向量的运算法则作出向量图,由勾股定理可得
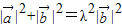 ,
,设向量
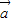 +
+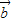 与
与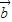 -
-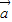 的夹角为θ,
的夹角为θ,
则cosθ=
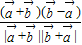 =
=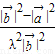
=
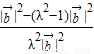 =
=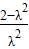 =
=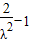 ,
,∵λ≥2,∴λ2≥4,0<
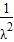
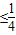 ,
,∴-1<
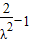
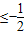 ,即-1<cosθ
,即-1<cosθ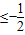 ,
,又θ∈[0,π],所以
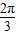 ≤θ≤π,
≤θ≤π,故向量
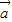 +
+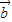 与
与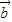 -
-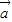 的夹角的最小值为
的夹角的最小值为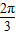
故答案为:
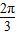
点评:本题考查数量积表示向量的夹角,涉及向量的模长和三角函数的取值范围,属中档题.

练习册系列答案
相关题目