题目内容
已知函数f（x）=
，判断f（x）在［2，+∞）上的单调性，并给出证明.
解：f（x）在［２，＋∞）上是单调递增的.
证明：任取2≤x1＜x2，f（x1）-f（x2）
=
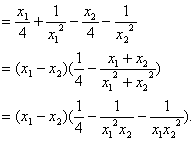
∵2≤x1＜x2，
∴x1-x2＜0,x1x22>8,x12x2>8，
即
.
∴
∴f（x1）-f（x2）＜0.
故而f（x）在[2，+∞)上单调递增.
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|