Question

10．已知函数f（x）=lnx-ax，a∈R．
（1）当a=1时，求f（x）的极值；
（2）讨论函数y=f（x）的零点个数．

Answer 1

分析 （1）求得a=1的函数的导数，求得单调区间，即可得到极值；
（2）令y=0，进行变形lnx=ax，即a=$\frac{lnx}{x}$，令 g（x）=$\frac{lnx}{x}$，利用导数的方法，研究其单调性及最大值，从而讨论a的范围，进而得到零点的个数．

解答 解：（1）a=1时，f（x）=lnx-x，x＞0，
导数f′（x）=$\frac{1}{x}$-1=$\frac{1-x}{x}$，
当x＞1时，f′（x）＜0，f（x）递减；
当0＜x＜1时，f′（x）＞0，f（x）递增，
即有x=1处取得极大值，且为-1；
无极小值；
（2）令f（x）=lnx-ax=0，则a=$\frac{lnx}{x}$，
令 g（x）=$\frac{lnx}{x}$，g′（x）=$\frac{1-lnx}{{x}^{2}}$，
解g′（x）=0得x=e．
则g（x）在（0，e）上单调递增，
在（e，+∞）上单调递减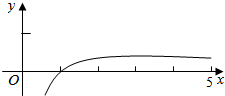
当x=e时，g（x）的最大值为g（e）=$\frac{1}{e}$，
g（x）的图象如右图．
即有当a＞$\frac{1}{e}$时，f（x）无零点；
当0＜a＜$\frac{1}{e}$时，y=a和y=g（x）两个交点，f（x）有两个零点；
当a=$\frac{1}{e}$或a≤0，y=a和y=g（x）一个交点，f（x）有一个零点．

点评 本题考查导数的运用：求单调区间和极值、最值，考查函数的零点的判断方法：数形结合，属于中档题．