题目内容
有如下列命题:
①三边是连续的三个自然数,且最大角是最小角的2倍的三角形存在且唯一;
②若
•
≥|
|•|
|,则存在正实数λ,使得
=λ
;
③若函数f(x)=
x3-ax2+(a2+3a-3)x+1在点x=1处取得极值,则实数a=1或a=-2;
④函数f(x)=x-sinx有且只有一个零点.
其中正确命题的序号是
①三边是连续的三个自然数,且最大角是最小角的2倍的三角形存在且唯一;
②若
| a |
| b |
| a |
| b |
| a |
| b |
③若函数f(x)=
| 1 |
| 3 |
④函数f(x)=x-sinx有且只有一个零点.
其中正确命题的序号是
①④
①④
.分析:①利用余弦定理进行判断.②利用数量积的定义和公式进行判断.③利用导数和极值的关系判断.④利用导数判断函数的单调性即可.
解答:解:①设三角形三边是连续的三个自然n-1,n,n+1,三个角分别为α,π-3α,2α,由正弦定理可得
=
=
,∴cosα=
.
再由余弦定理可得 (n-1)2=(n+1)2+n2-2(n+1)n•cosα,即 (n-1)2=(n+1)2+n2-2(n+1)n
.化简可得n2-5n=0,∴n=5. 此时,三角形的三边分别为:4,5,6,可以检验最大角是最小角的2倍.综上,存在一个三角形三边长分别为 4,5,6,且最大角是最小角的2倍.所以①正确.
②若
•
≥|
|•|
|,所以当
=
满足条件,所以②错误.
③函数的导数为f'(x)=x2-2ax+a2+3a-3,因为点x=1处取得极值,所以f'(1)=1-2a+a2+3a-3=0,解得a=1或a=-2,当a=1时,f'(x)=x2-2x+1=(x-1)2≥0,此时函数单调递增,无极值,所以③错误.
④函数的导数为f'(x)=1-cosx≥0,所以函数f(x)=x-sinx单调递增,因为f(0)=0,所以函数f(x)=x-sinx有且只有一个零点,正确.
故答案为:①④.
| n-1 |
| sin?α |
| n+1 |
| sin?2α |
| n+1 |
| 2sin?αcos?α |
| n+1 |
| 2(n-1) |
再由余弦定理可得 (n-1)2=(n+1)2+n2-2(n+1)n•cosα,即 (n-1)2=(n+1)2+n2-2(n+1)n
| n+1 |
| 2(n-1) |
②若
| a |
| b |
| a |
| b |
| b |
| 0 |
③函数的导数为f'(x)=x2-2ax+a2+3a-3,因为点x=1处取得极值,所以f'(1)=1-2a+a2+3a-3=0,解得a=1或a=-2,当a=1时,f'(x)=x2-2x+1=(x-1)2≥0,此时函数单调递增,无极值,所以③错误.
④函数的导数为f'(x)=1-cosx≥0,所以函数f(x)=x-sinx单调递增,因为f(0)=0,所以函数f(x)=x-sinx有且只有一个零点,正确.
故答案为:①④.
点评:本题主要考查各种命题的真假判断,涉及的知识点较多,综合性较强,难度较大.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,则存在正实数
,则存在正实数 ,使得
,使得 ;③若函数
;③若函数 在点
在点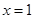 处取得极值,则实数
处取得极值,则实数 或
或 ;④函数
;④函数 有且只有一个零点.其中正确命题的序号是
.
有且只有一个零点.其中正确命题的序号是
.