题目内容
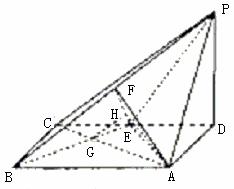
 四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点。
四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点。
(Ⅰ)求证:EF⊥平面PAB;
(Ⅱ)设AB=![]() BC,求AC与平面AEF所成的角的大小。
BC,求AC与平面AEF所成的角的大小。
方法一:
(Ⅰ)证明:连结EP,
∵PD⊥底面ABCD,DE在平面ABCD内,
∴PD⊥DE.又CE=ED,PD=AD=BC,∴Rt△BCE≌Rt△PDE.∴PE=BE.
∵F为PB中点, ∴EF⊥PB.
由三垂线定理得PA⊥AB,
∴在Rt△PAB中PF=AF,又PE=BE=EA,∴△EFP≌△EFA,∴EF⊥FA.
∵PB、FA为平面PAB内的相交直线,∴EF⊥平面PAB.
(Ⅱ)解:不妨设BC=1,则AD=PD=1,AB=![]() ,PA=
,PA=![]() ,AC=
,AC=![]() .
.
∴△PAB为等腰直角三角形,且PB=2,F为其斜边中点,BF=1,且AF⊥PB.
∵PB与平面AEF内两条相交直线EF、AF都垂直,∴PB⊥平面AEF.
连结BE交AC于G,作GH∥BP交EF于H,则GH⊥平面AEF. ∠GAH为AC与平面AEF所成的角.
由△EGC∽△BGA可知EG=![]() GB,EG=
GB,EG=![]() EB,AG=
EB,AG=![]() AC=
AC=![]() .
.
由△EGH∽△EBF可知GH=![]() BF=
BF=![]() .∴sin∠GAH=
.∴sin∠GAH=![]() .
.
AC与平面AEF所成的角为arcsin![]() .
.
方法二:
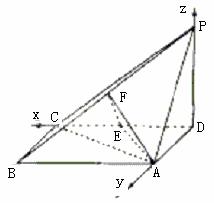
以D为坐标原点,DA的长为单位,建立如图所示的直角坐标系.
(Ⅰ)证明:
设E(a,0,0),其中a>0,则C(2a,0,0),A(0,1,0),B(2a,1,0),P(0,0,1),F(a,![]() ,
,![]() ).
).
![]() =(0,
=(0,![]() ,
,![]() ),
),![]() =(2a,1,-1),
=(2a,1,-1),![]() =(2a,0,0).
=(2a,0,0). ![]() ?
?![]() =0,
=0,
∴EF⊥PB. ![]() ?
?![]() =0, ∴EF⊥AB.
=0, ∴EF⊥AB.
又PB![]() 平面PAB,AB
平面PAB,AB![]() 平面PAB,PB∩AB=B,∴EF⊥平面PAB. ……6
平面PAB,PB∩AB=B,∴EF⊥平面PAB. ……6
(Ⅱ)解:由AB=![]() BC,得a=
BC,得a=![]() .
.
可得![]() =(
=(![]() ,-1,0),
,-1,0), ![]() =(
=(![]() ,1,-1),cos<
,1,-1),cos<![]() ,
,![]() >=
>=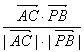 =
=![]()
异面直线AC、PB所成的角为arccos![]() .
. ![]() =(
=(![]() ,-
,-![]() ,
,![]() ),
),
∴![]() ?
?![]() =0,PB⊥AF.
=0,PB⊥AF.
又PB⊥EF,EF、AF为平面AEF内两条相交直线,∴PB⊥平面AEF.
∴AC与平面AEF所成的角为![]() -arccos
-arccos![]() (=arcsin
(=arcsin![]() ).
).
即AC与平面AEF所成的角为arcsin![]() .
.

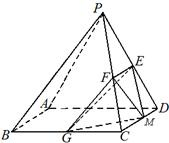 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.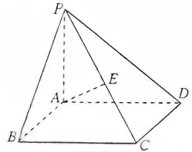 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2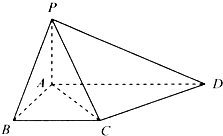 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.