题目内容
12.在△ABC中,边a,b,c分别为角A,B,C的对边,若a=$\sqrt{3}$,∠A=$\frac{π}{3}$,则当b取最大值时,△ABC的面积为$\frac{\sqrt{3}}{2}$.分析 由正弦定理可得$\frac{\sqrt{3}}{sin\frac{π}{3}}=\frac{b}{sinB}$,B=90°时,b的最大值为2,c=1,即可求出当b取最大值时,△ABC的面积.
解答 解:由正弦定理可得$\frac{\sqrt{3}}{sin\frac{π}{3}}=\frac{b}{sinB}$,
∴b=2sinB,
当B=90°时,sinB最大为1,故b的最大值为2,c=1,
∴当b取最大值时,△ABC的面积为$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查正弦定理,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.设x,y满足y=-x+1,则x2+y2的最小值为( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | 2 |
1.若P是正四面体V-ABC的侧面VBC上一点,点P到平面ABC的距离与到点V的距离相等,则动点P的轨迹为( )
| A. | 一条线段 | B. | 椭圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |

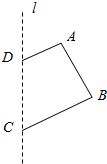 如图,直角梯形ABCD中,AB⊥BC,绕着CD所在直线l旋转,指出所得到的几何体的结构特征.
如图,直角梯形ABCD中,AB⊥BC,绕着CD所在直线l旋转,指出所得到的几何体的结构特征.