题目内容
关于x的方程8sin(x+
)cosx-2
-a=0在开区间(-
,
)上.
(1)若方程有解,求实数a的取值范围.
(2)若方程有两个不等实数根,求实数a的取值范围.
| π |
| 3 |
| 3 |
| π |
| 4 |
| π |
| 4 |
(1)若方程有解,求实数a的取值范围.
(2)若方程有两个不等实数根,求实数a的取值范围.
分析:(1)先对已知函数化简,由题意可得,4sin(2x+
)=a,由x的范围先求出2x+
π的范围,结合正弦函数的性质可求a的范围
(2)作出函数y=4sin(2x+
)在(-
,
)上图象,结合图象可求a的范围
| π |
| 3 |
| 1 |
| 3 |
(2)作出函数y=4sin(2x+
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
解答:解:(1)∵8sin(x+
)cosx-2
-a=0
∴4sinxcosx+4
cos2x-2
-a=0
∴2sin2x+2
cos2x=a
∴4sin(2x+
)=a
∵-
<x<
∴-
<2x+
<
π
∴-2<4sin(2x+
)≤4
∴-2<a≤4
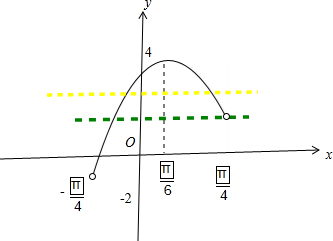
(2)图象法:函数y=4sin(2x+
)在(-
,
)上图象如图所示
由图象可得:a的取值范围为(2,4)
| π |
| 3 |
| 3 |
∴4sinxcosx+4
| 3 |
| 3 |
∴2sin2x+2
| 3 |
∴4sin(2x+
| π |
| 3 |
∵-
| π |
| 4 |
| π |
| 4 |
∴-
| π |
| 6 |
| π |
| 3 |
| 5 |
| 6 |
∴-2<4sin(2x+
| π |
| 3 |
∴-2<a≤4
(2)图象法:函数y=4sin(2x+
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
由图象可得:a的取值范围为(2,4)

点评:本题主要考查了辅助角公式的及正弦函数的性质的简单应用,体现了数 形结合思想的应用.

练习册系列答案
相关题目