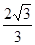题目内容
(12分)已知椭圆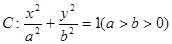 的离心率
的离心率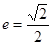 ,过右焦点
,过右焦点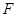 的直线
的直线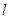 与椭圆
与椭圆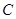 相交于
相交于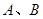 两点,当直线
两点,当直线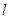 的斜率为1时,坐标原点
的斜率为1时,坐标原点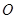 到直线
到直线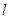 的距离为
的距离为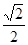 .
.
(1)求椭圆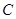 的方程
的方程
(2)椭圆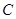 上是否存在点
上是否存在点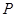 ,使得当直线
,使得当直线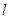 绕点
绕点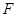 转到某一位置时,有
转到某一位置时,有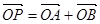 成立?若存在,求出所有满足条件的点
成立?若存在,求出所有满足条件的点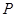 的坐标及对应直线方程;若不存在,请说明理由。
的坐标及对应直线方程;若不存在,请说明理由。
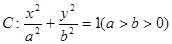 的离心率
的离心率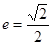 ,过右焦点
,过右焦点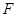 的直线
的直线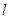 与椭圆
与椭圆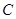 相交于
相交于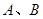 两点,当直线
两点,当直线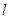 的斜率为1时,坐标原点
的斜率为1时,坐标原点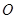 到直线
到直线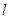 的距离为
的距离为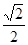 .
.(1)求椭圆
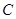 的方程
的方程(2)椭圆
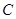 上是否存在点
上是否存在点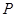 ,使得当直线
,使得当直线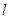 绕点
绕点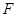 转到某一位置时,有
转到某一位置时,有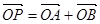 成立?若存在,求出所有满足条件的点
成立?若存在,求出所有满足条件的点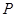 的坐标及对应直线方程;若不存在,请说明理由。
的坐标及对应直线方程;若不存在,请说明理由。(1)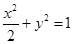 (2)存在,坐标为
(2)存在,坐标为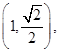 或
或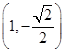 .
.
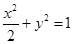 (2)存在,坐标为
(2)存在,坐标为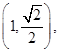 或
或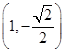 .
.试题分析:(1)因为直线
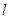 过右焦点
过右焦点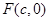 ,斜率为1,
,斜率为1,所以直线
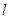 的方程为:
的方程为: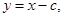 即
即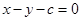 .
.坐标原点
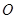 到直线
到直线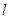 的距离为
的距离为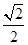 ,所以
,所以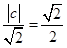 ,所以
,所以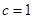 . …2分
. …2分因为离心率为
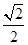 ,所以
,所以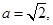 所以
所以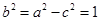 ,
,所以椭圆C的方程为
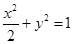 . …4分
. …4分(2)因为直线
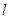 过右焦点,所以当直线
过右焦点,所以当直线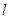 斜率不存在时,直线
斜率不存在时,直线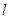 方程为:
方程为: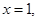
所以
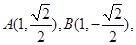 所以
所以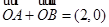 ,
,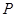 为右端点时,
为右端点时,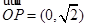 ,
,所以此时没有符合要求的点
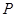 .
.当直线
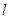 斜率存在时,设直线
斜率存在时,设直线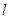 方程为:
方程为: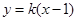 ,
,由
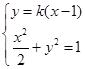 得:
得: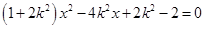 . …7分
. …7分设点
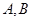 的坐标分别为
的坐标分别为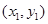 ,
,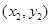 ,
,则
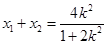 ,因为
,因为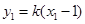 ,
,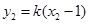 ,
,所以
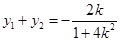 ,
,所以
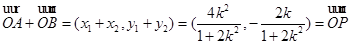 ,
,所以点
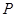 的坐标为
的坐标为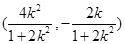 ,且符合椭圆方程,
,且符合椭圆方程,所以
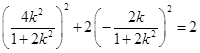 ,解得
,解得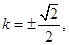
所以点
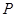 的坐标为
的坐标为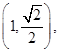 或
或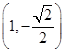 . …12分
. …12分点评:设直线方程时要注意斜率存在与不存在两种情况,求解直线与椭圆位置关系问题时,通常要联立方程组,运算量比较大,应该仔细计算,并且要注意通性通法的应用,加强解题的规范性.

练习册系列答案
相关题目
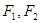 是双曲线
是双曲线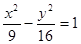 的两个焦点,点
的两个焦点,点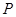 在双曲线上,且
在双曲线上,且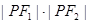
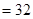 ,求证:
,求证:
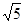 ,离心率
,离心率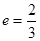 的椭圆两焦点为
的椭圆两焦点为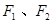 , 过
, 过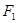 作直线交椭圆于
作直线交椭圆于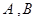 两
两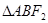 的周长为( )
的周长为( ) 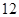
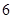
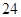
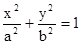 (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为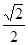 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N.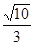 时,求k的值.
时,求k的值.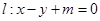 与抛物线
与抛物线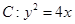 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。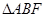 的重心G的轨迹方程;
的重心G的轨迹方程;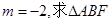 的外接圆的方程。
的外接圆的方程。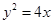 的焦点为
的焦点为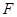 ,过点
,过点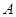 ,
,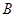 两点.
两点.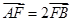 ,求直线
,求直线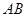 的斜率;
的斜率;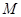 在线段
在线段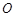 关于点
关于点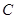 ,求四边形
,求四边形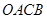 面积的最小值.
面积的最小值.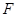 是抛物线
是抛物线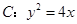 的焦点,过
的焦点,过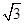 的直线交
的直线交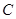 于
于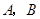 两点.设
两点.设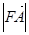 <
<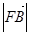 ,若
,若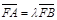 ,则λ的值为 .
,则λ的值为 . 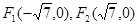 离心率e=
离心率e=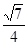 (1)求椭圆的方程。(2)若CD为过左焦点
(1)求椭圆的方程。(2)若CD为过左焦点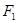 的弦,求
的弦,求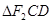 的周长
的周长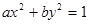 与直线
与直线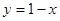 交于
交于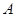
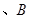 两点,过原点与线段
两点,过原点与线段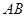 中点的直线的斜率为
中点的直线的斜率为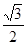 ,则
,则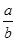 的值为 ( )
的值为 ( )