题目内容
定义一个对应法则f:P(m,n)→P(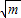 ,
,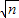 ),(m≥0,n≥0).现有点A(2,6)与点B(6,2),点M是线段AB上一动点,按定义的对应法则f:M→M′.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为 .
),(m≥0,n≥0).现有点A(2,6)与点B(6,2),点M是线段AB上一动点,按定义的对应法则f:M→M′.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为 .
【答案】分析:本题以定义的一种新的变换为入手点,主要考查直线与圆的有关知识,解答本题的关键是弄懂定义的本质,由定义的新法则f:P(m,n)→P(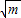 ,
,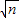 )(m≥0,n≥0).点A(2,6)与点B(6,2),点M是线段AB上一动点,而不难知道由变换得到点的轨迹是圆的一部分.然后根据弧长公式,易得答案.
)(m≥0,n≥0).点A(2,6)与点B(6,2),点M是线段AB上一动点,而不难知道由变换得到点的轨迹是圆的一部分.然后根据弧长公式,易得答案.
解答:解:由题意知AB的方程为:x+y=8,
设M(x,y),则M′(x2,y2),从而有x2+y2=8,
易知 A(2,6)→A′(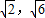 ),B(6,2)→B′(
),B(6,2)→B′(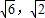 ),
),
不难得出∠A′OX=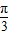 ,∠B′OX=
,∠B′OX=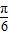 ,则∠A′OB′=
,则∠A′OB′=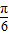 ,点M的对应点M′所经过的路线长度为
,点M的对应点M′所经过的路线长度为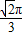 ;
;
故答案为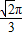 .
.
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.弄懂定义的本质是解题关键;针对本题,通过阅读题意,不难知道由变换得到点的轨迹是圆的一部分.
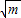 ,
,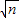 )(m≥0,n≥0).点A(2,6)与点B(6,2),点M是线段AB上一动点,而不难知道由变换得到点的轨迹是圆的一部分.然后根据弧长公式,易得答案.
)(m≥0,n≥0).点A(2,6)与点B(6,2),点M是线段AB上一动点,而不难知道由变换得到点的轨迹是圆的一部分.然后根据弧长公式,易得答案.解答:解:由题意知AB的方程为:x+y=8,
设M(x,y),则M′(x2,y2),从而有x2+y2=8,
易知 A(2,6)→A′(
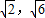 ),B(6,2)→B′(
),B(6,2)→B′(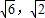 ),
),不难得出∠A′OX=
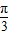 ,∠B′OX=
,∠B′OX=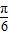 ,则∠A′OB′=
,则∠A′OB′=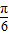 ,点M的对应点M′所经过的路线长度为
,点M的对应点M′所经过的路线长度为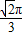 ;
;故答案为
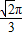 .
.点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果.弄懂定义的本质是解题关键;针对本题,通过阅读题意,不难知道由变换得到点的轨迹是圆的一部分.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目