题目内容
2. 下列三个图分别是四棱锥A-BCEF的直观图、侧视图、俯视图,在直观图中,侧面ABC⊥底面BCEF,M为AC的中点,侧视图是等边三角形,俯视图是直角梯形,有关数据如图所示.
下列三个图分别是四棱锥A-BCEF的直观图、侧视图、俯视图,在直观图中,侧面ABC⊥底面BCEF,M为AC的中点,侧视图是等边三角形,俯视图是直角梯形,有关数据如图所示.(1)求证:BM∥面AEF;
(2)求证:AE⊥BM;
(3)求该四棱锥A-BCEF的体积.
分析 (1)取AE的中点N,连结MN,FN,证明:四边形BMNF为平行四边形,可得FN∥BM,即可证明BM∥面AEF;
(2)证明BM⊥平面ACE,即可证明AE⊥BM;
(3)取BC的中点O,连结AO,证明AO⊥底面BCEF,即可求该四棱锥A-BCEF的体积.
解答  (1)证明:取AE的中点N,连结MN,FN
(1)证明:取AE的中点N,连结MN,FN
在△ACE中,∵M为AC的中点,
∴MN∥CE且MN=$\frac{1}{2}$CE=1,
∵BF∥CE,BF=$\frac{1}{2}$CE=1,
∴MN∥BF,MN=BF,
∴四边形BMNF为平行四边形,
∴FN∥BM,
∵FN?面AEF,BM?面AEF,
∴BM∥面AEF;
(2)解:∵∠BCE=90°,侧面△ABC⊥底面BCEF,
∴CE⊥平面ABC,∴CE⊥BM,
又△ABC是正三角形,M为AC的中点,∴BM⊥AC,
∵AC∩CE=C,∴BM⊥平面ACE,
∴AE⊥BM;
(3)解:取BC的中点O,连结AO,
∵△ABC是边长为2的正三角形,
∴AO⊥BC,AO=$\sqrt{3}$,
又侧面△ABC⊥底面BCEF,
∴AO⊥底面BCEF,
∴四棱锥A-BCEF的体积V=$\frac{1}{3}×\frac{1}{2}×(1+2)×2×\sqrt{3}$=$\sqrt{3}$.
点评 本题考查线面平行、垂直的判定,考查四棱锥A-BCEF的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
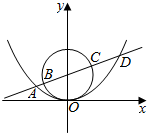 如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )
如图所示,过抛物线x2=4py(p>0)焦点的直线依次交抛物线与圆x2+(y-p)2=p2于点A,B,C,D,则$\overrightarrow{AB}$•$\overrightarrow{CD}$的值是( )