题目内容
已知函数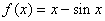
，则
．
.
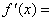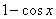【解析】
试题分析：两函数的差求导数.分别求导再相减.故填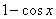.正弦函数的导数是余弦函数.
考点：1.函数的差的求导方法.2.正弦函数的导数.
练习册系列答案
英才计划期末调研系列答案
精英口算卡系列答案
相关题目
英才计划期末调研系列答案精英口算卡系列答案题目内容
已知函数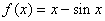，则 ．
.
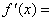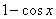【解析】
试题分析：两函数的差求导数.分别求导再相减.故填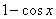.正弦函数的导数是余弦函数.
考点：1.函数的差的求导方法.2.正弦函数的导数.
英才计划期末调研系列答案精英口算卡系列答案
,函数
在区间
上的最大值等于
，则
的值为 ． 
：任意
，
，命题
：函数
在
上单调递减．
的取值范围；
的图象在点
处的切线方程为
，则函数
的图象在点
处的切线方程为 .
，若焦点在
轴上的椭圆
过点
，且其长轴长等于圆
的直径．
作两条互相垂直的直线
与
，
、
两点， 
，设直线
，求弦
长；
面积的最大值．
的离心率
，A,B是椭圆的左、右顶点，P是椭圆上不同于A,B的一点，直线PA,PB倾斜角分别为
，则
，且AB＝2AD＝2DC＝2PD＝4，E为PA的中点．
的方程
有实根，则
的取值范围是________．
的两条渐近线将平面划分为“上、下、左、右”四个区域（不含边界），若点(1, 2)在“上”区域内，则双曲线离心率的取值范围为 。